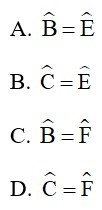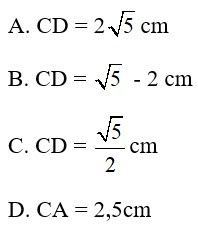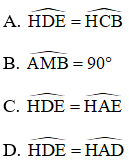35 câu trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác (có đáp án).docx

35 câu trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác (có đáp án) chọn lọc

Bài 1: Tam giác ABC có A ^=2B^, AC = 16cm, BC = 20cm. Tính độ dài cạnh AB.

Bạn đang đọc: 35 câu trắc nghiệm Trường hợp đồng dạng thứ ba của tam giác (có đáp án).docx

A. 18 cm
B. 20 cm
C. 15 cm
D. 9 cm

Đáp án: D

Bài 2: Cho tam giác ABC vuông tại A có: AB = 5, AC = 12. Trên cạnh BC lấy điểm M

sao cho BM = 513 BC. Qua M kẻ đường thẳng vuông góc với AC tại N. Độ dài MN là :
A. 1213
B. 4513
C. 4013
D. 12

Đáp án: C

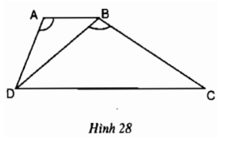
Bài 3 : Cho hình thang vuông ABCD ( A ^ = D ^ = 900 )
có BC BD, AB = 4 cm, CD = 9 cm. Độ dài BD là :
A. 8 cm
B. 12 cm
C. 9 cm
D. 6 cm

Đáp án: D

Bài 4: Cho hai tam giác ABC và FED có A ^=F^, cần thêm điều kiện gì dưới đây để hai tam giác (thứ tự đỉnh như vậy) đồng dạng theo trường hợp góc – góc?

Đáp án: A

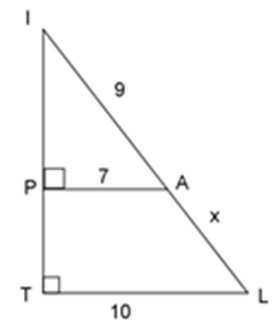
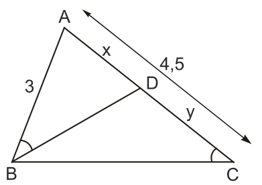
Bài 5: Tính giá trị của x trong hình dưới đây:

A. x = 3
B.x = 277
C. x = 4
D. x = 275

Đáp án: B

Bài 6: Tam giác ABC có A ^=2B^, AB = 11cm, AC = 25cm. Tính độ dài cạnh BC.

A. 30 cm
B. 20 cm
C. 25 cm
D. 15 cm

Đáp án: A

Bài 7: Nếu 2 tam giác ABC và DEF có A^=70°,C^=60°,E^=50°,F^=70° thì chứng minh được:

A. ΔABC ~ ΔFED
B. ΔACB ~ ΔFED
C. ΔABC ~ ΔDEF
D. ΔABC ~ ΔDFE

Đáp án: A

Bài 8: Cho tam giác ABC cân tại A. Trên cạnh AC lấy điểm M, trên đoạn thẳng BM lấy điểm K sao cho góc BCK^=ABM^ .

1. Tam giác MBC đồng dạng với tam giác
A. MCK
B. MKC
C. KMC
D. CMK

Đáp án: A

2. Tính MB.MK bằng
A. 2MC2
B. CA2
C. MC2
D. BC2

Đáp án: C

Bài 9: Cho hình thang ABCD (AB // CD) có góc ADB^=BCD^, AB = 2cm, BD = 5cmm, ta có:

Đáp án: D

Bài 10: Cho ΔABC có các đường cao BD và CE cắt nhau tại H. Gọi M là giao của AH với BC.

1. Chọn câu đúng .
A. ΔHBE ~ ΔHCD
B. ΔABD ~ ΔACE
C. Cả A, B đều đúng
D. Cả A, B đều sai

Đáp án: C

2. Chọn khẳng định sai.

Đáp án: D

Bài 11: Cho hình bình hành ABCD, điểm F trên cạnh BC. Tia AF cắt BD và DC lần lượt ở E và G. Chọn khẳng định sai.

A. ΔBFE ~ ΔDAE
B. ΔDEG ~ ΔBEA
C. ΔBFE ~ ΔDEA
D. ΔDGE ~ ΔBAE

Đáp án: C

Bài 12: Cho hình bình hành ABCD có I là giao điểm của AC và BD. E là một điểm bất kì thuộc BC, qua E kẻ đường thẳng song song với AB và cắt BD, AC, AD tại G, H, F. Chọn kết luận sai?

A. ΔBGE ~ ΔHGI
B. ΔGHI ~ ΔBAI
C. ΔBGE ~ ΔDGF
D. ΔAHF ~ ΔCHE

Đáp án: A

Bài 13: Nếu 2 tam giác ABC và DEF có A^=D^,C^=F^ thì:

A. ΔABC ~ ΔDEF
B. ΔCAB ~ ΔDEF
C. ΔABC ~ ΔDFE
D. ΔCBA ~ ΔDFE

Đáp án: A

Bài 14: Cho ΔABC có đường cao AD, CE và trực tâm H.

1. Chọn câu vấn đáp đúng nhất .
A. ΔADB ~ ΔCDH
B. ΔABD ~ ΔCBE
C. Cả A, B đều đúng
D. Cả A, B đều sai

Đáp án: C

2. Chọn khẳng định sai.

                                         

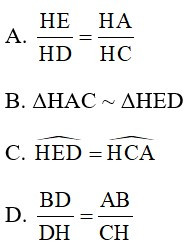
Đáp án: C

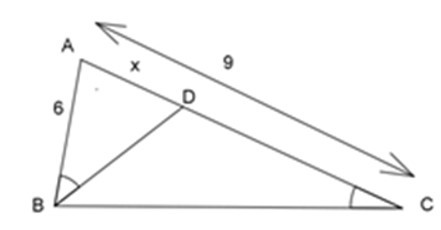
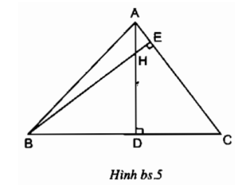
Bài 15: Cho hình bên biết AB = 6cm, AC = 9cm,ABD^=BCA^. Độ dài đoạn AD là:

Xem thêm: Phân tích các nguyên tắc hoạt động của doanh nghiệp trong cơ chế thị trường và – Tài liệu text – Chia Sẻ Kiến Thức Điện Máy Việt Nam – Kiến Thức Cho Người lao Động Việt Nam

A. 2 cm
B. 3 cm
C. 4 cm
D. 5 cm

Đáp án: C

Bài 16: Cho ΔABC cân tại A, M là trung điểm BC, BC = 2a

lấy D, E thuộc AB, AC sao cho DME ^ = ABC ^. Tính BD.CE bằng
A. 2 a2
B. 3 a
C. a2
D. 4 a2

Đáp án: C

Bài 17: Cho hình bên biết AB = 8cm, AC = 16cm, ABD^=BCA^. Độ dài đoạn AD là:

A. 4 cm
B. 8 cm
C. 6 cm
D. 5 cm

Đáp án: A

Bài 18: Cho tam giác ABC cân tại A, M là trung điểm của BC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho DM là tia phân giác của BDE. Chọn khẳng định đúng.

Đáp án: C

Bài 19: Cho 2 tam giác ABC và DEF

có A ^ = 40 °, B ^ = 80 °, E ^ = 40 °, D ^ = 60 °. Chọn câu đúng .
A. ΔABC ~ ΔDEF
B. ΔFED ~ ΔCBA
C. ΔACB ~ ΔEFD
D. ΔDFE ~ ΔCBA

Đáp án: D

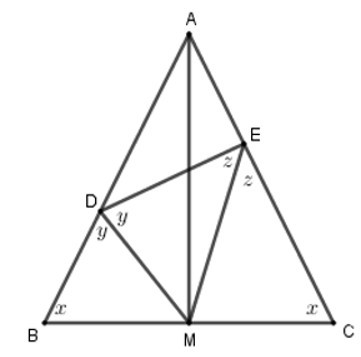
Bài 20: Cho tam giác ABC cân tại A, M là trung điểm của BC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho DM là tia phân giác của BDE. Chọn kết luận đúng.

A. ΔBDM ~ ΔCME
B. ΔBDM ~ ΔEMC
C. ΔBDM ~ ΔCEM
D. ΔBDM ~ ΔECM

Đáp án: A

Bài 21: Cho ΔABC cân tại A, có BC = 2a, M là trung điểm BC,

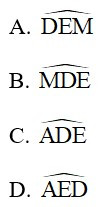
lấy D, E thuộc AB, AC sao cho DME ^ = ABC ^. Góc BDM bằng với góc nào dưới đây ?

Đáp án: B

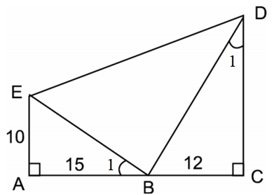
Bài 22: Cho AE = 10cm, AB = 15cm, BC = 12cm. Hãy tính độ dài các đoạn thẳng CD (làm tròn đến chữ số thập phân thứ nhất)

A. 16cm

B. 12cm

C. 18cm

D. 20cm

Đáp án: C

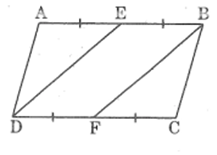
Bài 23: Cho hình bình hành ABCD .Gọi E là trung điểm của AB, F là trung điểm của CD. Chọn câu trả lời đúng?

A. ΔAED ∽ ΔCFB
B. ΔADE ∽ ΔCFB
C. ΔAED ∽ ΔCBF
D. ΔADE ∽ ΔCFB

Đáp án: A

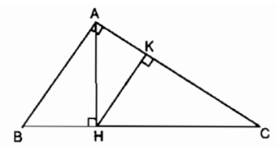
Bài 24: Tam giác vuông ABC có A^ = 90° và đường cao AH. Từ H hạ HK vuông góc với AC. Trong hình đã cho có bao nhiêu tam giác đồng dạng với nhau?

A. 1
B. 2
C. 3
D. 4

Đáp án: A

Bài 25: Hình thang ABCD (AB // CD) có AB = 2,5cm, AD = 3,5cm, BD = 5cm và DAB^=DBC^.Tính độ dài BC.

A. 8 cm
B. 10 cm
C. 7 cm
D. 5 cm

Đáp án: C

Bài 26: Cho biết tam giác ABC có hai đường cao AD và BE cắt nhau tại H.

Trong hình có số cặp tam giác đồng dạng với nhau là :
A. 1 cặp
B. 6 cặp
C. 3 cặp
D. 4 cặp

Đáp án: B

Bài 27: Hình thang vuông ABCD (AB // CD) có đường chéo BD vuông góc với cạnh BC tại B và có độ dài BD = m = 7,25cm. Hãy tính độ dài các cạnh của hình thang, biết rằng BC = n = 10,75cm

A. 11,29cm

B. 12,97cm

C. 18cm

D. 4,05cm

Đáp án: B

Bài 28: Cho biết AB = 3cm; AC = 4,5cm và. Cho biết thêm BD là tia phân giác của góc B. Hãy tính độ dài các đoạn thẳng BC.

A. 2 cm
B. 4 cm
C. 3,75 cm
D. 2,5 cm

Đáp án: C

Bài 29: Cho biết . Cho biết AE = 10cm, AB = 15cm, BC = 12cm. Hãy tính độ dài các đoạn thẳng CD

A. 26,63 cm
B. 18,03 cm
C. 28,18 cm
D. 21,63 cm

Đáp án: D

Bài 30: Cho hai tam giác ABC và FED có ABC^=FED^ , cần thêm điều kiện gì dưới đây để hai tam giác (thứ tự đỉnh như vậy) đồng dạng theo trường hợp góc – góc? 

A. ACB ^ = FED ^

B. ABC^=FDE^

Xem thêm: Trái phiếu doanh nghiệp là gì? Có gì khác với trái phiếu chính phủ?

C. ACB ^ = FDE ^
D.ACB ^ = DFE ^

Đáp án: C

Source: https://vh2.com.vn
Category : Doanh Nghiệp