[SGK Scan] ✅ Dãy số có giới hạn hữu hạn – Sách Giáo Khoa – Học Online Cùng https://vh2.com.vn

Xem thêm các sách tham khảo liên quan:

Bạn đang đọc: [SGK Scan] ✅ Dãy số có giới hạn hữu hạn – Sách Giáo Khoa – Học Online Cùng https://vh2.com.vn

Xem thêm: Phân tích các nguyên tắc hoạt động của doanh nghiệp trong cơ chế thị trường và – Tài liệu text – Chia Sẻ Kiến Thức Điện Máy Việt Nam – Kiến Thức Cho Người lao Động Việt Nam

Xem thêm: TIẾP THỊ & QUẢNG CÁO | Business Owner Space

Dãy số có giới hạn hữu hạn –
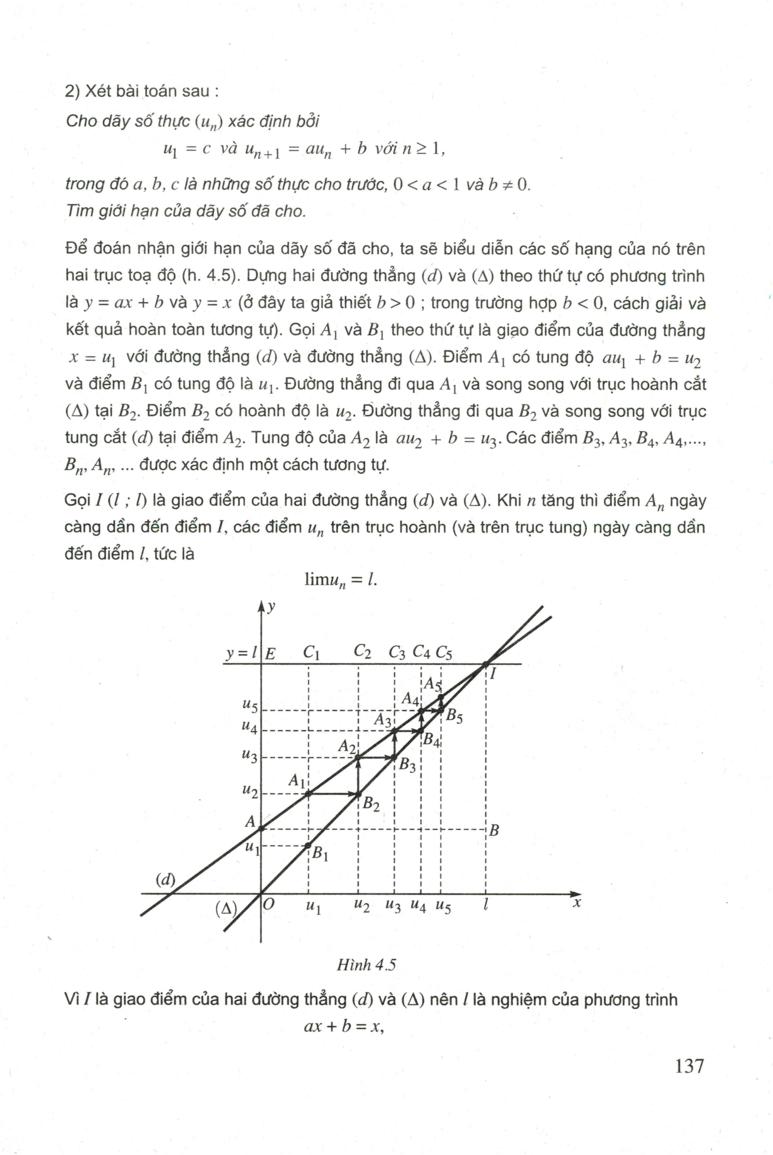
Định nghĩa dãy số có giới hạn hữu hạn. Xét dãy số u ( n ) với u ( n ) = 3 + ( ( – 1 ) ^ n ) / n. Ta có lim ( u ( n ) – 3 ) = lim ( ( – 1 ) ^ n ) / n = 0. Ta nói rằng dãy số u ( n ) có giới hạn là 3. Một cách tổng quát, ta có : ĐINH NGHIA Ta nói rằng dãy số ( un ) có giới hạn là số thực L nếu lim ( u, – L ) = 0. Khi đó ta viết lim ( u, ) = L hoặc limu ) = L hoặc lin -> L.Dãy số có giới hạn là một số thực gọi là dãy số có giới hạn hữu hạm. Ví dụ 1. Dãy số không đổi ( u, .. ) với u, = C ( c là hằng số ) có giới hạn là C vìlim ( u, – c ) = lim ( c. – c ) = lim0 = 0. O – Ví dụ 2. Chứng minh rằng lim ( – ) – 1 = – 1. Gidi Đặt u = 与颍 – 1. 1. V li A – I :. 1 – ) م ( ” – isyen : – im ( u, – ( – 1 ) ) = limo : Z ~ = 0, nên limu, = – 1. D н1 Chứng minh rằng : ( ү эүп ) a ) lim ( ) — 1 ) = 1 ; b ) im ( ? – Nhận xét 1 ) Từ định nghĩa vừa nêu, suy ra rằng limun = L khi và chỉ khi khoảng chừng cáchịu, – L từ điểm u, đến điểm L trở nên nhỏ bao nhiêu cũng được miễn là m đủ lớn ; nói một cách hình ảnh, khi n tăng những điểm u, chụm lại quanh điểm L. 2 ) Không phải mọi dãy số đều có giới hạn hữu hạn. Chẳng hạn dãy số ( ( – 1 ) ” ), tức là dãy số-1, 1, – 1, 1, …. không có giới hạn hữu hạn. 1312. Trên trục số, những số hạng của dãy số đó được màn biểu diễn bởi hai điểm – 1 và 1. Khi n tăng những điểm ( – 1 ) ” không chụm lại quanh bất kỳ một điểm L nào. Một số định lí Ta thừa nhận những định lí sauĐINH LÍ1Giả sử limu, = L. Khi đó a ) limu, = | L | và lim Q. / u, = RL ; b ) Nếu u, > 0 với mọi n thì L > 0 và lim Nu, = VL, Ví dụ 3. imyo 02 = 3 Vì im ( 9 — = 9. 2H2 Tim limit – n : ĐINH LÍ2Giả sử limu, = L, limy = M và c là một hằng số. Khi đó lim ( u, + v, ) = L + M, lim ( u, , — v, ) = L — M, lim ( u, … vi ) = LM, lim ( cut ) = CL, L – ܩܠܐ ܕin limặ = # ( nếu M + 0 ). 24 nVí dụ4. Tìm limu, với u, — ” “, ” “, GiảiTa cólimu, = im ( a – = lim3 + lim ; lim = im3 + 4 im – 7 lin = 3 + 40-70 = 3,1323. 2 Ví dụ 5. Tìm limu, với t, = * * * *. n ” – 5 n + 7 Gidi Chia tử và mẫu của phân thức cho lũy thừa bậc cao nhất của n trong tử và mẫu của phân thức ), ta được4 3 3. 2 – + + 구 lu, = 1 –. .. n Vì m — = im2 – lin + in + lin = 2 Jገ n * n ዘገ 2 + و4 – 3 và im ( 1-3 + 1 ) = I zonën limo * * * * * * * * = P = 2 D no – 5 + 7 1 no-n + 3 | H3. Tìm giới hạn của dãy số ( u, ) với u, = ” + ” : ”. no + 2 nTổng của cấp số nhân lùi vô hạn Xét cấp số nhân vô hạn 2 ս, սլզ, սլզ ՞ … սլզ ”, … có công bội q với | q | < 1 ( gọi là một cấp số nhân lùi vô hạn ). Ta biết rằng tổng của n số hạng tiên phong của cấp số nhân đó là — и, ( 1 — q " ) И, и, Sn = uլ + սլզ + ... + սլզ " " = - 1 - q1-d n. Vì | q | < 1 nên limạ ” = 0. Do đó - llim S. 유, - Ta gọi giới hạn đó là tổng của cấp số nhân đã cho và viết + ° tባq + tባq + ܨS - u133 5.6. Tìm tổng của cấp số nhân22 23V í dụ 6. Biểu diễn số thập phân vô hạn tuần hoàn 0,777. dưới dạng phân số. 去 ... Gidi Ta có 0,777 ... = 乱 -- -- Đây là tổng của một cấp số nhân lùi vô hạn với số hạng đầu u1 = 斋 Và công bội q 一击 Do đó • 7. 7 0.777. o, 9 OO | H5l Biểu diễn số thập phân vô hạn tuẩn hoàn 0,313131 ... dưới dạng phân sốCâu hủi và bài tậpTìm những giới hạn sau : ( - 1 ) ". „ ( sin 3 n - 1 ). a ) lim | 2 b ) im ( 4 n c ) lim " : d ) lim ". n + 1 Tìm limu, với 2 2 n-3n+5 一2n ^ + n + 2 a ) u = H – ; b ) u = -- H ; ' 2 ? - 1 " 3 n + 5 4. " c ) I = --- ; d ) μ = -. ) lu, " 2 ვ " + 4 " 7.9.1. Cho dãy số ( un ) xác lập bởi lu4 = 10 và 14,11 - - 3 với mọi n > 1. a ) Chứng minh rằng dãy số ( yn ) xác lập bởi Vn = u, – 巽 là một cấp số nhân. b ) Tìm limu, Cho một tam giác đều ABC cạnh a, Tam giác ABC, có những đỉnh là trung điểm những cạnh của tam giác ABC, tam giác A, B, C, có những đỉnh là trung điểm những cạnh của tam giác A, B, C1, …, tam giác A, 1B, 11C, 1 có những đỉnh là trung điểm những cạnh của tam giác A, B, C, , … .. Gọi p1, p. 2, … p, … và USD 1, USD 2, … S, … theo thứ tự là chu vi và diện tích quy hoạnh của những tam giác ABC, A2 B2C2, …, A, B, Cո … .. a ) Tìm giới hạn của những dãy số ( p ) và ( Sn ). b ) Tìm những tổngp1 + p2 + ・ + pn + … va S + S2 + ・ + Sa + … Biểu diễn những số thập phân vô hạn tuần hoàn sau dưới dạng phân số : a ) 0.444 … ; b ) 0,2121 … ; c ) 0,32111 …. Gọi C là nửa đường tròn đường kính AB = 2F, C1 là đường gồm hai nửa đường tròn đường kínhoC2 là đường gồm bốn nửa đường tròn đường kính 学 – – – C, là đường gồm 2 ” nửa đường tròn đường kính, … ( h. 4.2 ). Gọi p, là độ dài của Cn, S, là diện tích quy hoạnh hình phẳng giới hạn bởi C, và đoạn thẳng AB.a ) Tính p, và S. b ) Tìm giới hạn của những dãy số ( pg ) và ( Sn ). Hình 4.2 ĐOÁN NHÂN GIỞI HAN CỦA MộT DÂY SỐ THƯC BẢNG HìNH HQC1 ) Ta đã biết tổng của cấp số nhân lùi vô hạn 2 ′ ? ‘ 23 ” “ ; “ 1. 1 + ܚs = ਨ ੂ ੰ 2. ( xem trong USD 2 ). Có thể đoán nhận được hiệu quả này nhờ hình 4.3 hoặc hình 44. + … = 1 lill lllll Ο 2 ਨ ੂ ੰ ਨ ੂ ੰ ਨ ੂ ੰ ਨ ੂ ੰ Hình 4,3 Ở hình 4.3 : trung điểm của đoạn [ 0 ; 1 ] là điểm i. trung điểm của đoạn là diém 블 – truna điểm của đoan 블-1 là điểm — – 부 trung 2 2 2 22 23 ”. Do đó1 1 ਨ ੂ ੰ = IỞ hình 44 : hình vuông vắn ABCD có cạnh 却 6 dài 1 đơn vị chức năng và diện tích quy hoạnh bằng 1, hình 1. chữ nhật AEFB có diện tích quy hoạnh bằng 1. hình vuông vắn DHGE có diện tích quy hoạnh bằng E若一 hình chữ nhật GIKF có diện tíchbằng 부, – – – – 2 2D o đó – — – A. 2 – 2 Hình 442 ). Xét bài toán sau : Cho dãy số thực ( u, ) xác lập bởiιι ) = ο να μη, 1 = αι., + b νόή η > 1, trong đó a, b, c là những số thực cho trước, 0 < a < 1 và b = 0. Tìm giới hạn của dãy số đã cho. Để đoán nhận giới hạn của dãy số đã cho, ta sẽ trình diễn những số hạng của nó trên hai trục tọa độ ( h, 4.5 ). Dựng hai đường thẳng ( d ) và ( A ) theo thứ tự có phương trình là y = ax + b và y = \ ( ở đây ta giả thiết b > 0 ; trong trường hợp b < 0, cách giải và hiệu quả trọn vẹn tương tự như ). Gọi Al và B, theo thứ tự là giao điểm của đường thẳng x = u, với đường thẳng ( d ) và đường thẳng ( A ). Điểm A có tung độ aut + b = u2 và điểm B có tung độ là u1. Đường thẳng đi qua AI và song song với trục hoành cắt ( A ) tại B ). Điểm B, có hoành độ là u2. Đường thẳng đi qua B, và song song với trục tung cắt ( d ) tại điểm A2, Tung độ của A2 là au2 + b = ua. Các điểm B3, A2, B1, A4, ..., B, An, ... được xác lập một cách tương tự như. Gọi I ( I, I ) là giao điểm của hai đường thẳng ( d ) và ( A ). Khi n tăng thì điểm A, ngày càng dần đến điểm I, những điểm u, trên trục hoành ( và trên trục tung ) ngày càng dần đến điểm I, tức làlimu, = l. Hình 4-5 Vì I là giao điểm của hai đường thẳng ( d ) và ( A ) nên I là nghiệm của phương trình ax + b = x, 137 Cho một tam giác đều ABC cạnh a. Tam giác A1B1C1, có những đỉnh là trung điểm những cạnh của tam giác ABC, tam giác A2B2C2 có những đỉnh là trung điểm những cạnh của tam giác A1B1C1, ..., tam giác A ( n + 1 ) B ( n + 1 ) C ( n + 1 ) có những đỉnh là trung điểm những cạnh của tam giác A ( n ) B ( n ) C ( n ), ..... Gọi p1, p2, ... p ( n ), ... và S1, S2, ... S ( n ), ... theo thứ tự là chu vi và diện tích quy hoạnh của những tam giác A1B1C1, A2B2C2, ..., A ( n ) B ( n ) C ( n ) ..... a ) Tìm giới hạn của những dãy số p ( n ) và ( Sn ). b ) Tìm những tổng ?

Source: https://vh2.com.vn
Category : Doanh Nghiệp