PHẦN III-HỆ TRỤC TỌA ĐỘ TRONG KHÔNG GIAN OXYZ

PHẦN 7. HỆ TRỤC TỌA ÐỘ TRONG KHÔNG GIAN OXYZ

1. HỆ TỌA ĐỘ KHÔNG GIAN

1.1.1.  Khái niệm mở đầu

Trong không gian cho ba trục $Ox,Oy,Oz$ phân biệt và vuông góc từng đôi một. Gốc tọa độ $O,$ truc hoành $Ox,$ trục tung $Oy,$ trục cao $Oz,$ các mặt tọa độ $\left( Oxy \right),\left( Oyz \right),\left( Ozx \right).$

1.1.2. Khái niệm về hệ trục tọa độ

Khi không gian có hệ tọa độ thì gọi là không gian tọa độ $ Oxyz $ hay không gian USD Oxyz. $

Chú ý:       

1.1.3. Tọa độ véc tơ              

1.1.4. Tọa độ điểm               

1.1.5. Các công thức tọa độ cần nhớ

Cho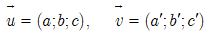 

• USD \ vec { u } = \ vec { v } \ Leftrightarrow \ left \ { \ begin { align } và a = a ‘ \ \ và b = b ‘ \ \ và c = c ‘ \ \ \ end { align } \ right. $

• 

• USD k \ overrightarrow { u } = \ left ( ka ; \ kb ; \ kc \ right ) USD

• USD \ overrightarrow { u } \ overrightarrow { v } = \ left | \ overrightarrow { u } \ right | \ left | \ overrightarrow { v } \ right |. \ cos \ left ( \ overrightarrow { u }, \ overrightarrow { v } \ right ) = aa ‘ + bb ‘ + cc ‘ $

• USD \ cos \ left ( \ overrightarrow { u }, \ overrightarrow { v } \ right ) = \ frac { \ overrightarrow { u } \ overrightarrow { v } } { \ left | \ overrightarrow { u } \ right | \ left | \ overrightarrow { v } \ right | } = \ frac { aa ‘ + bb ‘ + cc ‘ } { \ left | \ overrightarrow { u } \ right | \ left | \ overrightarrow { v } \ right | } $

• USD \ left | \ overrightarrow { u } \ right | = \ sqrt { { { \ overrightarrow { u } } ^ { 2 } } } = \ sqrt { { { a } ^ { 2 } } + { { b } ^ { 2 } } + { { c } ^ { 2 } } } $

• USD \ overrightarrow { u } \ bot \ overrightarrow { v } \ Leftrightarrow \ overrightarrow { u } \ overrightarrow { v } = 0 USD

• USD \ overrightarrow { AB } = \ left ( { { x } _ { B } } – { { x } _ { A } } ; \ { { y } _ { B } } – { { y } _ { A } } ; \ { { z } _ { B } } – { { z } _ { A } } \ right ) USD

• USD AB = \ left | \ overrightarrow { AB } \ right | = \ sqrt { { { \ left ( { { x } _ { B } } – { { x } _ { A } } \ right ) } ^ { 2 } } + { { \ left ( { { y } _ { B } } – { { y } _ { A } } \ right ) } ^ { 2 } } + { { \ left ( { { z } _ { B } } – { { z } _ { A } } \ right ) } ^ { 2 } } } $

1.1.6. Chú ý

1.1.7. Chia tỉ lệ đoạn thẳng

M chia AB theo tỉ số k nghĩa là 

Công thức tọa độ của M là : 

1.1.8. Công thức trung điểm

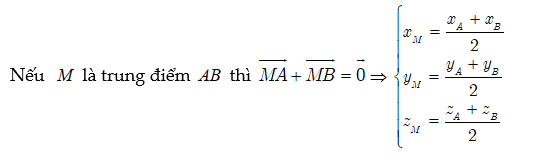
1.1.9. Công thức trọng tâm tam giác

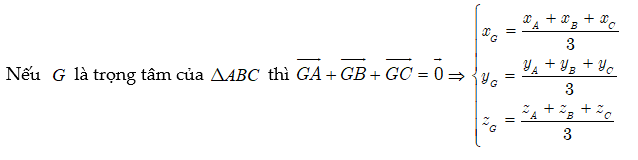
1.1.10. Công thức trọng tâm tứ diện

1.1.11. Tích có hướng 2 véc tơ

1.1.12. Tính chất tích có hướng 2 véc tơ

• • USD \ left [ \ vec { u }, \ vec { v } \ right ] $

    vuông góc với $ \ vec { u } $ và $ \ vec { v } $

  • USD \ left | \ left [ \ vec { u }, \ vec { v } \ right ] \ right | = \ left | { \ vec { u } } \ right |. \ left | { \ vec { v } } \ right | \ sin \ left ( \ vec { u }, \ vec { v } \ right ) USD

  • USD \ left [ \ vec { u }, \ vec { v } \ right ] = \ vec { 0 } \ Leftrightarrow \ vec { u }, \ vec { v } $ cùng phương

1.1.13. Ứng dụng tích có hướng 2 véc tơ

1.2.1. Các phép toán về toạ độ của vectơ và của điểm

Phương pháp giải

• • Sử dụng những công thức về toạ độ của vectơ và của điểm trong không gian .

  • Sử dụng những phép toán về vectơ trong không gian .

1.2.2. Xác định điểm trong không gian. Chứng minh tính chất hình học. Diện tích – Thể tích

Phương pháp giải

• • Sử dụng những công thức về toạ độ của vectơ và của điểm trong không gian .

  • Sử dụng những phép toán về vectơ trong không gian .

  • Công thức xác lập toạ độ của những điểm đặc biệt quan trọng .

  • Tính chất hình học của những điểm đặc biệt quan trọng :

• USD A, \, B, \, C $ thẳng hàng $ \ Leftrightarrow \ overrightarrow { AB } ; \ \ overrightarrow { AC } $ cùng phương $ \ Leftrightarrow \ overrightarrow { AB } = k \ overrightarrow { AC } \ Leftrightarrow \ left [ \ overrightarrow { AB } ; \ \ overrightarrow { AC } \ right ] = \ overrightarrow { 0 } $

• USD ABCD $ là hình bình hành $ \ Leftrightarrow \ overrightarrow { AB } = \ overrightarrow { DC } $

• Cho  $\Delta ABC$ có các chân  $E;\ F$ của các đường phân giác trong và ngoài của góc $A$  của $\Delta ABC$  trên $BC$.

Ta có : $ \ overrightarrow { EB } = \ frac { – AB } { AC }. \ overrightarrow { EC } ; \ \ \ \ \ overrightarrow { FB } = \ frac { AB } { AC }. \ overrightarrow { FC } $

• USD A, \, B, C, D $ không đồng phẳng $ \ Leftrightarrow \ overrightarrow { AB } ; \ \ overrightarrow { AC } ; \ \ overrightarrow { AD } $ không đồng phẳng

USD \ Leftrightarrow \ left [ \ overrightarrow { AB }, \ overrightarrow { AC } \ right ]. \ overrightarrow { AD } \ ne 0 USD

2.1.5.  Những trường hợp riêng của  phương trình tổng quát

• $ \ left ( P \ right ) USD qua gốc tọa độ

   

  USD \ Leftrightarrow D = 0 USD

• $ \ left ( P \ right ) USD song song hoặc trùng $ \ left ( Oxy \ right ) \ Leftrightarrow A = B = 0 USD

• $ \ left ( P \ right ) USD song song hoặc trùng $ \ left ( Oyz \ right ) \ Leftrightarrow B = C = 0 USD

• $ \ left ( P \ right ) USD song song hoặc trùng $ \ left ( Ozx \ right ) \ Leftrightarrow A = C = 0 USD

• $ \ left ( P \ right ) USD song song hoặc chứa $ Ox \ Leftrightarrow A = 0 USD

• $ \ left ( P \ right ) USD song song hoặc chứa USD Oy \ Leftrightarrow B = 0 USD

• $ \ left ( P \ right ) USD song song hoặc chứa USD Oz \ Leftrightarrow C = 0 USD

• $ \ left ( P \ right ) USD cắt $ Ox $ tại $ A \ left ( a ; 0 ; 0 \ right ), USD cắt $ Oy $ tại $ B \ left ( 0 ; b ; 0 \ right ) USD và cắt $ Oz $ tại $ C \ left ( 0 ; 0 ; c \ right ) \ Leftrightarrow \ left ( P \ right ) USD có phương trình $ \ frac { x } { a } + \ frac { y } { b } + \ frac { z } { c } = 1 \ \ \ \ left ( a, b, c \ \ ne 0 \ right ) USD

2.1.6.  Khoảng cách từ 1 điểm đến mặt phẳng

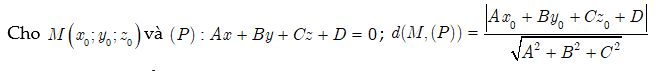
2.1.7.  Chùm mặt phẳng

Để lập phương trình mặt phẳng $\left( \alpha  \right)$ ta cần xác định một điểm thuộc $\left( \alpha  \right)$ và một VTPT của nó.

2.2.1. Dạng 1

$\left( \alpha  \right)$ đi qua điểm  $M\left( {{x}_{0}};\ {{y}_{0}};{{z}_{0}} \right)$ có VTPT  $\overrightarrow{n}=\left( A;B;C \right)$ thì:

$\left( \alpha  \right):\ A\left( x-{{x}_{0}} \right)+B\left( y-{{y}_{0}} \right)+C\left( z-{{z}_{0}} \right)=0$

2.2.2. Dạng 2

$\left( \alpha  \right)$ đi qua điểm $M\left( {{x}_{0}};\ {{y}_{0}};{{z}_{0}} \right)$ có cặp VTCP $\overrightarrow{a},\overrightarrow{b}$ thì $\overrightarrow{n}=\left[ \overrightarrow{a},\overrightarrow{b} \right]$ là  một VTPT của  $\left( \alpha  \right)$

2.2.3. Dạng 3

$ \ left ( \ alpha \ right ) USD đi qua điểm USD M \ left ( { { x } _ { 0 } } ; \ { { y } _ { 0 } } ; { { z } _ { 0 } } \ right ) USD và song song với $ \ left ( \ beta \ right ) : Ax + By + Cz = 0 $ thì $ \ left ( \ alpha \ right ) : \ A \ left ( x – { { x } _ { 0 } } \ right ) + B \ left ( y – { { y } _ { 0 } } \ right ) + C \ left ( z – { { z } _ { 0 } } \ right ) = 0 $ $ $

2.2.4. Dạng 4

$\left( \alpha  \right)$ đi qua 3 điểm không thẳng hàng $A,\ B,\ C$. Khi đó ta có thể xác định một VTPT của $\left( \alpha  \right)$ là: $\overrightarrow{n}=\left[ \overrightarrow{AB},\overrightarrow{AC} \right]$

2.2.5. Dạng 5

$\left( \alpha  \right)$ đi qua một điểm $M$ và một đường thẳng $\left( d \right)$ không chứa $M$:

• Trên $ \ left ( \ alpha \ right ) USD lấy điểm $ A $

  và VTCP $ \ overrightarrow { u } $ .

• Một VTPT của $ \ left ( \ alpha \ right ) USD là : $ \ overrightarrow { n } = \ left [ \ overrightarrow { AM }, \ overrightarrow { u } \ right ] $

2.2.6. Dạng 6

$\left( \alpha  \right)$ đi qua một điểm $M$, vuông góc với đường thẳng $\left( d \right)$ thì VTCP $\overrightarrow{u}$ của đường thẳng $\left( d \right)$ là một VTPT của $\left( \alpha  \right)$.

2.2.7. Dạng 7

$\left( \alpha  \right)$ chứa đường thẳng cắt nhau ${{d}_{1}},\ {{d}_{2}}$

• Xác định những VTCP $ \ overrightarrow { a }, \ \ overrightarrow { b } $ của những đường thẳng $ { { d } _ { 1 } }, \ { { d } _ { 2 } }. $

• Một VTPT của $ \ left ( \ alpha \ right ) USD là : $ \ overrightarrow { n } = \ left [ \ overrightarrow { a }, \ overrightarrow { b } \ right ] $

• Lấy một điểm USD M $ thuộc d1 hoặc $ { { d } _ { 2 } } \ Rightarrow M \ in \ left ( \ alpha \ right ) USD

2.2.8. Dạng 8

$\left( \alpha  \right)$ chứa đường thẳng ${{d}_{1}}$ và song song với đường thẳng ${{d}_{2}}$ (${{d}_{1}},{{d}_{2}}$ chéo nhau:

• Xác định những VTCP $ \ overrightarrow { a }, \ \ overrightarrow { b } $ của những đường thẳng $ { { d } _ { 1 } }, \ { { d } _ { 2 } }. $

• Một VTPT của $ \ left ( \ alpha \ right ) USD là : $ \ overrightarrow { n } = \ left [ \ overrightarrow { a }, \ \ overrightarrow { b } \ right ] $

• Lấy một điểm USD M $ thuộc $ { { d } _ { 1 } } \ Rightarrow M \ in \ left ( \ alpha \ right ) USD

2.2.9. Dạng 9

$\left( \alpha  \right)$ đi qua điểm $M$ và song song với hai đường thẳng chéo nhau ${{d}_{1}},{{d}_{2}}$:

• Xác định những VTCP $ \ overrightarrow { a }, \ \ overrightarrow { b } $

  của những đường thẳng $ { { d } _ { 1 } }, \ { { d } _ { 2 } }. $

• Một VTPT của $ \ left ( \ alpha \ right ) USD là : $ \ overrightarrow { n } = \ left [ \ overrightarrow { a }, \ \ overrightarrow { b } \ right ] $ .

2.2.10. Dạng 10

$ \ left ( \ alpha \ right ) USD chứa một đường thẳng USD d USD và vuông góc với một mặt phẳng $ \ left ( \ beta \ right ) USD

• Xác định VTCP $ \ overrightarrow { u } $

  của USD d USD và VTPT $ \ overrightarrow { { { n } _ { \ beta } } } $ của $ \ left ( \ beta \ right ) USD

• Một VTPT của $ \ left ( \ alpha \ right ) USD là : $ \ overrightarrow { n } = \ left [ \ overrightarrow { u }, \ \ overrightarrow { { { n } _ { \ beta } } } \ right ] $

• Lấy một điểm USD M USD thuộc USD d \ Rightarrow M \ in \ left ( \ alpha \ right ) USD

2.2.11. Dạng 11

$\left( \alpha  \right)$ đi qua điểm $M$ và vuông góc với hai mặt phẳng cắt nhau $\left( \beta  \right),\ \left( \gamma  \right):$

• Xác định những VTPT $ \ overrightarrow { { { n } _ { \ beta } } }, \ \ overrightarrow { { { n } _ { \ gamma } } } $

  của $ \ left ( \ beta \ right ) USD

  và $ \ left ( \ gamma \ right ) USD

• Một VTPT của $ \ left ( \ alpha \ right ) USD là : $ \ overrightarrow { n } = \ left [ \ overrightarrow { { { u } _ { \ beta } } }, \ \ overrightarrow { { { n } _ { \ gamma } } } \ right ] $

2.2.12. Dạng 12

$\left( \alpha  \right)$ chứa đường thẳng $d$  cho trước và cách điểm $M$  cho trước một khoảng $k$ cho trước:

• Giả sử $ \ left ( \ alpha \ right ) USD

  có phương trình : USD Ax + By + Cz + D = 0 \ \ \ left ( { { A } ^ { 2 } } + { { B } ^ { 2 } } + { { C } ^ { 2 } } \ ne 0 \ right ) USD

• Lấy 2 điểm $ AB \ in \ left ( d \ right ) \ Rightarrow A, \ B \ in \ left ( \ alpha \ right ) USD

  (

  ta được hai phương trình $ \ left ( 1 \ right ), \ left ( 2 \ right ) USD )

• Từ điều kiện kèm theo khoảng cách USD d \ left ( M, \ \ left ( \ alpha \ right ) \ right ) = k USD, ta được phương trình ( 3 ) .

• Giải hệ phương trình $ \ left ( 1 \ right ), \ left ( 2 \ right ), \ left ( 3 \ right ) USD ( bằng cách cho giá trị một ẩn, tìm những ẩn còn lại ) .

2.2.13. Dạng 13

$\left( \alpha  \right)$ là tiếp xúc với mặt cầu $\left( S \right)$ tại điểm $H.$

• Giả sử mặt cầu $ \ left ( S \ right ) USD

  có tâm USD I $ và nửa đường kính $ R $

• Một VTPT của $ \ left ( \ alpha \ right ) USD là : $ \ overrightarrow { n } = \ overrightarrow { IH } $

Cho hai mặt phẳng $ \ left ( P \ right ) : Ax + By + Cz + D = 0 $ và $ \ left ( P ‘ \ right ) : \ A’x + B’y + C’z + D ‘ = 0 USD
Khi đó :

• $ \ left ( P \ right ) USD

   cắt $\left( P’ \right)$

  USD \ Leftrightarrow A : B : C \ ne A ‘ : B ‘ : C ‘ $

• $ \ left ( P \ right ) / / \ left ( P ‘ \ right ) \ Leftrightarrow \ frac { A } { A ‘ } = \ frac { B } { B ‘ } = \ frac { C } { C ‘ } \ ne \ frac { D } { D ‘ } $

• $ \ left ( P \ right ) \ equiv \ left ( P ‘ \ right ) \ Leftrightarrow \ frac { A } { A ‘ } = \ frac { B } { B ‘ } = \ frac { C } { C ‘ } = \ frac { D } { D ‘ } $

• $ \ left ( P \ right ) \ bot \ left ( P ‘ \ right ) \ Leftrightarrow { { \ overrightarrow { n } } _ { \ left ( P \ right ) } } \ bot { { \ overrightarrow { n } } _ { \ left ( P ‘ \ right ) } } \ Leftrightarrow { { \ overrightarrow { n } } _ { \ left ( P \ right ) } }. { { \ overrightarrow { n } } _ { \ left ( P ‘ \ right ) } } = 0 \ Leftrightarrow AA ‘ + BB ‘ + CC ‘ = 0 USD

2.4.1.  Khoảng cách từ 1 điểm đến 1 mặt phẳng

Khoảng cách từ điểm $ { { M } _ { 0 } } \ left ( { { x } _ { 0 } } ; { { y } _ { 0 } } ; { { z } _ { 0 } } \ right ) USD đến mặt phẳng $ \ left ( \ alpha \ right ) : \ Ax + By + Cz + D = 0 $ là USD d \ left ( { { M } _ { 0 } }, \ left ( \ alpha \ right ) \ right ) = \ frac { \ left | A { { x } _ { 0 } } + B { { y } _ { 0 } } + C { { z } _ { 0 } } + D \ right | } { \ sqrt { { { A } ^ { 2 } } + { { B } ^ { 2 } } + { { C } ^ { 2 } } } } $

2.4.2.  Khoảng cách giữa 2 mặt phẳng song song

Khoảng cách giữa hai mặt phẳng song song bằng khoảng cách từ một điểm bất kể trên mặt phẳng này đến mặt phẳng kia .

2.4.3.  Hình chiếu của 1 điểm lên mặt phẳng

Điểm $ H $ là hình chiếu của điểm USD M $ trên $ \ left ( P \ right ) \ Leftrightarrow \ \ overrightarrow { MH }, \ \ overrightarrow { n } $ cùng phương $ \ left ( H \ in \ left ( P \ right ) \ right ) USD

2.4.4.  Điểm đối xứng của 1 điểm qua mặt phẳng

Điểm USD M ‘ $ đối xứng với điểm USD M $ qua $ \ left ( P \ right ) \ Leftrightarrow \ overrightarrow { MM ‘ } = 2 \ overrightarrow { MH } $
Cho hai mặt phẳng $ \ left ( \ alpha \ right ), \ \ left ( \ beta \ right ) USD có phương trình : $ \ left ( \ alpha \ right ) : \ { { A } _ { 1 } } x + { { B } _ { 1 } } y + { { C } _ { 1 } } z + { { D } _ { 1 } } = 0 USD
USD \ \ \ \ left ( \ beta \ right ) : \ { { A } _ { 2 } } x + { { B } _ { 2 } } y + { { C } _ { 2 } } z + { { D } _ { 2 } } = 0 USD
Góc giữa $ \ left ( \ alpha \ right ), \ \ left ( \ beta \ right ) USD bằng hoặc bù với góc giữa hai VTPT $ \ overrightarrow { { { n } _ { 1 } } }, \ \ overrightarrow { { { n } _ { 2 } } } $ .

$\cos \left( \left( \alpha  \right),\left( \beta  \right) \right)=\frac{\left| \overrightarrow{{{n}_{1}}}.\overrightarrow{{{n}_{2}}} \right|}{\left| \overrightarrow{{{n}_{1}}} \right|.\left| \overrightarrow{{{n}_{2}}} \right|}=\frac{\left| {{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}} \right|}{\sqrt{{{A}_{1}}^{2}+{{B}_{1}}^{2}+{{C}_{1}}^{2}}+\sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}}$

Chú ý : USD { { 0 } ^ { 0 } } \ le \ left ( \ widehat { \ left ( \ alpha \ right ), \ left ( \ beta \ right ) } \ right ) \ le { { 90 } ^ { 0 } } $ ; $ \ left ( \ alpha \ right ) \ bot \ left ( \ beta \ right ) \ Leftrightarrow { { A } _ { 1 } } { { A } _ { 2 } } + { { B } _ { 1 } } { { B } _ { 2 } } + { { C } _ { 1 } } { { C } _ { 2 } } = 0 USD
Cho mặt phẳng $ \ left ( \ alpha \ right ) : \ Ax + By + Cz + D = 0 $ và mặt cầu $ \ left ( S \ right ) : \ { { \ left ( x-a \ right ) } ^ { 2 } } + { { \ left ( y-b \ right ) } ^ { 2 } } + { { \ left ( z-c \ right ) } ^ { 2 } } = { { R } ^ { 2 } } $ có tâm USD I USD

• $ \ left ( \ alpha \ right ) USD và $ \ left ( S \ right ) USD

  không có điểm chung $ \ Leftrightarrow d \ left ( I, \ left ( \ alpha \ right ) \ right ) > R USD

• $ \ left ( \ alpha \ right ) USD tiếp xúc với $ \ left ( S \ right ) \ Leftrightarrow d \ left ( I, \ left ( \ alpha \ right ) \ right ) = R $

  với $ \ left ( \ alpha \ right ) USD là tiếp diện

Để tìm toạ độ tiếp điểm ta hoàn toàn có thể thực thi như sau :

• Viết phương trình đường thẳng USD d USD đi qua tâm USD I $ của $ \ left ( S \ right ) USD và vuông góc với $ \ left ( \ alpha \ right ) USD .

• Tìm toạ độ giao điểm $ H $

  của USD d USD

  và $ \ left ( \ alpha \ right ) USD. $ H $

  là tiếp điểm của $ \ left ( S \ right ) USD

  với $ \ left ( \ alpha \ right ) USD .

• $ \ left ( \ alpha \ right ) USD cắt $ \ left ( S \ right ) USD

   theo một đường tròn $\Leftrightarrow d\left( I,\ \left( \alpha  \right) \right)

Để xác lập tâm $ H $ và nửa đường kính USD r USD của đường tròn giao tuyến ta hoàn toàn có thể triển khai như sau :

• Viết phương trình đường thẳng USD d USD đi qua tâm USD I USD

  của $ \ left ( S \ right ) USD và vuông góc với $ \ left ( \ alpha \ right ) USD .

• Tìm toạ độ giao điểm $ H $

  của USD d USD và $ \ left ( \ alpha \ right ) USD. Với $ H $ là tâm của đường tròn giao tuyến của $ \ left ( S \ right ) USD với $ \ left ( \ alpha \ right ) USD .

• Bán kính USD r USD

  của đường tròn giao tuyến : USD r = \ sqrt { { { R } ^ { 2 } } – I { { H } ^ { 2 } } } $

3.1.1. Vectơ chỉ phương của đường thẳng

3.1.1.1. Ðịnh nghĩa

3.1.1.2. Chú ý

3.1.2. Phương trình tham số của đường thẳng

3.1.3. Phương trình chính  tắc của đường thẳng

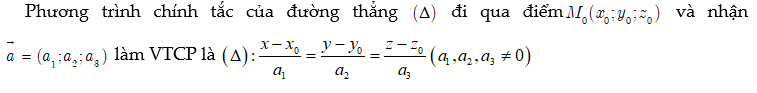
3.2.1. Vị trí tương đối của đường thẳng và mặt phẳng

3.2.1.1. Phương pháp hình học

Định lý

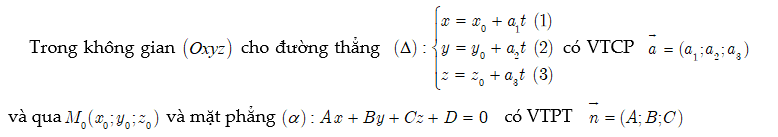
Khi đó :

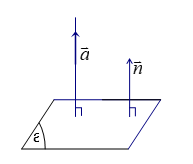
$ \ left ( \ Delta \ right ) \ cap \ left ( \ alpha \ right ) \ Leftrightarrow \ vec a. \ vec n \ ne 0 \ Leftrightarrow A { a_1 } + B { a_2 } + C { a_3 } \ ne 0 USD

$\left( \Delta  \right)//\left( \alpha  \right) \Leftrightarrow \left\{ \begin{array}{l}
\vec a.\vec n = 0\\
{M_0} \notin \left( P \right)
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
A{a_1} + B{a_2} + C{a_3} = 0\\
A{x_0} + B{y_0} + C{z_0} \ne 0
\end{array} \right.$

$\left( \Delta  \right) \subset \left( \alpha  \right) \Leftrightarrow \left\{ \begin{array}{l}
\vec a.\vec n = 0\\
{M_0} \in \left( P \right)
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
A{a_1} + B{a_2} + C{a_3} = 0\\
A{x_0} + B{y_0} + C{z_0} = 0
\end{array} \right.$

Đặc biệt

3.2.2. Vị trí tương đối của hai đường thẳng

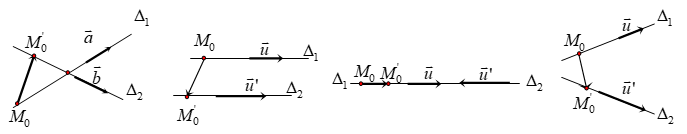
3.2.2.1. Phương pháp hình học

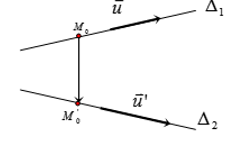
Cho hai đường thẳng : USD { { \ Delta } _ { 1 } } $ đi qua USD M $ và có một vectơ chỉ phương $ \ overrightarrow { { { u } _ { 1 } } } $
USD { { \ Delta } _ { 2 } } $ đi qua $ N $ và có một vectơ chỉ phương $ \ overrightarrow { { { u } _ { 2 } } } $

• USD { { \ Delta } _ { 1 } } \ equiv { { \ Delta } _ { 2 } } \ Leftrightarrow \ left [ \ overrightarrow { { { u } _ { 1 } } }, \ overrightarrow { { { u } _ { 2 } } } \ right ] = \ left [ \ overrightarrow { { { u } _ { 1 } } }, \ overrightarrow { MN } \ right ] = \ overrightarrow { 0 } $

      ${\Delta _1} /  / {\Delta _2} \Leftrightarrow \left\{ \begin{array}{l}
      \left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = \overrightarrow 0 \\
      \left[ {\overrightarrow {{u_1}} ,\overrightarrow {MN} } \right] \ne 0
      \end{array} \right.$

      ${\Delta _1} \cap {\Delta _2} \Leftrightarrow \left\{ \begin{array}{l}
      \left[ {\overrightarrow {{u_1}} ,\;\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \\
      \left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right].\overrightarrow {MN}  = 0
      \end{array} \right.$

• USD { { \ Delta } _ { 1 } } $

  và $ { { \ Delta } _ { 2 } } $ chéo nhau $ \ Leftrightarrow \ left [ \ overrightarrow { { { u } _ { 1 } } }, \ overrightarrow { { { u } _ { 2 } } } \ right ]. \ overrightarrow { MN } \ ne 0 USD

3.2.2.2. Phương pháp đại số

3.2.3. Vị trí tương đối giữa đường thẳng và mặt cầu

3.2.3.1. Phương pháp hình học

3.2.2.2. Phương pháp đại số

Thế ( 1 ), ( 2 ), ( 3 ) vào phương trình ( S ) và rút gọn đưa về phương trình bậc hai theo t ( * )

• Nếu phương trình $ \ left ( * \ right ) USD vô nghiệm thì d không cắt $ \ left ( S \ right ) USD

• Nếu phương trình ( * ) có một nghiệm thì s tiếp xúc ( S )

• Nếu phương trình ( * )

   có hai nghiệm thì d cắt ( S )

   tại hai điểm phân biệt M, N

  Xem thêm: Phân tích văn bản Thông tin về ngày trái đất năm 2000 – Trường THPT Thành Phố Sóc Trăng

Chú ý:

Ðể tìm tọa độ M, N ta thay giá trị t vào phương trình đường thẳng d

3.3 .Góc trong không gian

3.3.1. Góc giữa hai mặt phẳng

3.3.2. Góc giữa đường thẳng và mặt phẳng

3.3.3. Góc giữa hai đường thẳng

3.4.1. Khoảng cách từ một điểm đến một mặt phẳng

3.4.2. Khoảng cách từ một điểm đến một đường thẳng

3.4.3. Khoảng cách giữa đường thẳng chéo nhau

3.5 .Lập phương trình đường thẳng

Để lập phương trình đường thẳng USD d USD ta cần xác lập 1 điểm thuộc USD d USD và một VTCP của nó .

3.5.1. Dạng 1

$d$  đi qua điểm ${{M}_{0}}\left( {{x}_{0}};{{y}_{0}};{{z}_{0}} \right)$ và có VTCP $\overrightarrow{a}=\left( {{a}_{1}},{{a}_{2}},{{a}_{3}} \right)$  là.$\left( d \right):\left\{ \begin{array}{l}
x = {x_0} + {a_1}t\\
y = {y_0} + {a_2}t\\
z = {z_0} + {a_3}t
\end{array} \right.\;\;\;\left( {t \in } \right)$

3.5.2. Dạng 2

USD d USD đi qua hai điểm $ A, \ B : USD Một VTCP của USD d USD là $ \ overrightarrow { AB } $ .

3.5.3. Dạng 3

USD d USD đi qua điểm $ { { M } _ { 0 } } \ left ( { { x } _ { 0 } } ; { { y } _ { 0 } } ; { { z } _ { 0 } } \ right ) USD và song song với đường thẳng $ \ Delta $ cho trước : Vì $ d / / \ Delta $ nên VTCP của $ \ Delta $ cũng là VTCP của USD d USD .

3.5.4. Dạng 4

$d$ đi qua điểm  ${{M}_{0}}\left( {{x}_{0}};{{y}_{0}};{{z}_{0}} \right)$ và vuông góc với mặt phẳng $\left( P \right)$ cho trước: Vì $d\bot \left( P \right)$  nên VTPT của $\left( P \right)$ cũng là VTCP của $d$.

3.5.5. Dạng 5

USD d USD là giao tuyến của hai mặt phẳng $ \ left ( P \ right ), \ left ( Q \ right ) USD :

• Cách 1 :

Tìm một điểm và một VTCP .

• Tìm toạ độ một điểm $A\in d$ bằng cách giải hệ phương trình $\left\{ \begin{array}{l}
  \left( P \right)\\
  \left( Q \right)
  \end{array} \right.$  (với việc chọn giá trị cho một ẩn)

• Tìm một VTCP của USD d : \ overrightarrow { a } = \ left [ \ overrightarrow { { { n } _ { P } } }, \ overrightarrow { { { n } _ { Q } } } \ right ] $

• Cách 2 :

Tìm hai điểm $ A, \ B $ thuộc USD d USD, rồi viết phương trình đường thẳng đi qua hai điểm đó .

3.5.6. Dạng 6

$d$ đi qua điểm ${{M}_{0}}\left( {{x}_{0}};{{y}_{0}};{{z}_{0}} \right)$ và vuông góc với hai đường thẳng ${{d}_{1}},\ {{d}_{2}}:$  

Vì USD d \ bot { { d } _ { 1 } }, \ d \ bot { { d } _ { 2 } } $ nên một VTCP của USD d USD là : $ \ overrightarrow { a } = \ left [ \ overrightarrow { { { a } _ { 1 } } }, \ overrightarrow { { { a } _ { 2 } } } \ right ] $

3.5.7. Dạng 7

USD d USD đi qua điểm $ { { M } _ { 0 } } \ left ( { { x } _ { 0 } } ; { { y } _ { 0 } } ; { { z } _ { 0 } } \ right ) USD, vuông góc và cắt đường thẳng USD \ Delta $ .

• Cách 1 :

Gọi $H$ là hình chiếu vuông góc của ${{M}_{0}}$ trên đường thẳng $\Delta $. Thì $\left\{ \begin{array}{l}
H \in \Delta \\
\overrightarrow {{M_0}H}  \bot \overrightarrow {{u_\Delta }} 
\end{array} \right.$

• Cách 2 :

Gọi $\left( P \right)$ là mặt phẳng đi qua $A$ và vuông góc với $d$$,\ \left( Q \right)$  là mặt phẳng đi qua $A$ và chứa $d$.  Khi đó $d=\left( P \right)\cap \left( Q \right)$

3.5.8. Dạng 8

USD d USD đi qua điểm $ { { M } _ { 0 } } \ left ( { { x } _ { 0 } } ; { { y } _ { 0 } } ; { { z } _ { 0 } } \ right ) USD và cắt hai đường thẳng $ { { d } _ { 1 } }, \ { { d } _ { 2 } } : USD

• Cách 1 :

Gọi ${{M}_{1}}\in {{d}_{1}},\ {{M}_{2}}\in {{d}_{2}}.$ Từ điều kiện $M,\ {{M}_{1}},\ {{M}_{2}}$  thẳng hàng ta tìm được ${{M}_{1}},\ {{M}_{2}}$. Từ đó suy ra phương trình đường thẳng $d$.

• Cách 2 :

Gọi $ \ left ( P \ right ) = \ left ( { { M } _ { 0 } }, { { d } _ { 1 } } \ right ), \ \ left ( Q \ right ) = \ left ( { { M } _ { 0 } }, { { d } _ { 2 } } \ right ). $ Khi đó USD d = \ left ( P \ right ) \ cap \ left ( Q \ right ). $ Do đó, một VTCP của USD d USD hoàn toàn có thể chọn là $ \ overrightarrow { a } \ left [ \ overrightarrow { { { n } _ { P } } }, \ overrightarrow { { { n } _ { Q } } } \ right ] $ .

3.5.9. Dạng 9

$d$ nằm trong mặt phẳng $\left( P \right)$ và cắt cả hai đường thẳng ${{d}_{1}},\ {{d}_{2}}:$

Tìm các giao điểm $A={{d}_{1}}\cap \left( P \right),\ B={{d}_{2}}\cap \left( P \right).$

Khi đó  chính là đường thẳng $AB.$

3.5.10. Dạng 10

Viết phương trình mặt phẳng $\left( P \right)$ chứa $\Delta $ và ${{d}_{1}},$ mặt phẳng $\left( Q \right)$ chứa $\Delta $  và ${{d}_{2}}$. 

Khi đó USD d = \ left ( P \ right ) \ cap \ left ( Q \ right ) USD .

3.5.11. Dạng 11

$d$ là đường vuông góc chung của hai đường thẳng ${{d}_{1}},\ {{d}_{2}}$  chéo nhau:

• Cách 1 :

Gọi ${{M}_{1}}\in {{d}_{1}},\ {{M}_{2}}\in {{d}_{2}}.$ Từ điều kiện $\left\{ \begin{array}{l}
MN \bot {d_1}\\
MN \bot {d_2}
\end{array} \right.,$

• Cách 2 :

• Vì $\left\{ \begin{array}{l}
  d \bot {d_1}\\
  d \bot {d_2}
  \end{array} \right.$  nên một VTCP của $d$ có thể là: .$\overrightarrow a  = \left[ {{{\overrightarrow a }_{{d_1}}},{{\overrightarrow a }_{{d_2}}}} \right]$

• Lập phương trình mặt phẳng $ \ left ( P \ right ) USD

   

  chứa$d$và ${{d}_{1}},$ bằng cách:

• Lấy một điểm $ A $ trên $ { { d } _ { 1 } }. $

• Một VTPT của

  $ \ left ( P \ right ) USD 

  hoàn toàn có thể là : USD { { \ overrightarrow { n } } _ { P } } = \ left [ \ overrightarrow { a }, { { \ overrightarrow { a } } _ { { { d } _ { 1 } } } } \ right ] $ .

• Tương tự lập phương trình mặt phẳng $ \ left ( Q \ right ) USD chứa

  USD d USD

   

  và

  USD { { d } _ { 2 } }. $

  Khi đó USD d = \ left ( P \ right ) \ cap \ left ( Q \ right ) USD

  .

3.5.12. Dạng 12

$d$ là hình chiếu của đường thẳng $\Delta $ lên mặt phẳng $\left( P \right)$ thì ta Lập phương trình mặt phẳng $\left( Q \right)$ chứa $\Delta $ và vuông góc với mặt phẳng $\left( P \right)$ bằng cách:

• Lấy USD M \ in \ Delta $ .

• Vì $\left( Q \right)$ chứa $\Delta $  và vuông góc với $\left( P \right)$ nên ${{\overrightarrow{n}}_{Q}}=\left[ {{\overrightarrow{a}}_{\Delta }},{{\overrightarrow{n}}_{P}} \right]$.

• Khi đó USD d = \ left ( P \ right ) \ cap \ left ( Q \ right ) USD .

3.5.13. Dạng 13

$d$ đi qua điểm $M$, vuông góc với ${{d}_{1}}$ và cắt ${{d}_{2}}:$

• Cách 1 :

Gọi $N$ là giao điểm của$d$ và ${{d}_{2}}.$ Từ điều kiện $MN\bot {{d}_{1}}$, ta tìm được $N.$ Khi đó, $d$ là đường thẳng $MN$.

• Cách 2 :

• Viết phương trình mặt phẳng $\left( P \right)$ qua $M$ và vuông góc với ${{d}_{1}}$

• Viết phương trình mặt phẳng $\left( Q \right)$ chứa $M$ và ${{d}_{2}}.$

• Khi đó USD d = \ left ( P \ right ) \ cap \ left ( Q \ right ). $

3.6.1. Vị trí tương đối giữa hai đường thẳng

Để xét VTTĐ giữa hai đường thẳng, ta hoàn toàn có thể sử dụng một trong những giải pháp sau :

• Phương pháp hình học :

Dựa vào mối quan hệ giữa những VTCP và những điểm thuộc những đường thẳng .

• Phương pháp đại số :

Dựa vào số nghiệm của hệ phương trình những đường thẳng .

3.6.2. Vị trí tương đối giữa đường thẳng và mặt phẳng

Để xét VTTĐ giữa đường thẳng và mặt phẳng, ta hoàn toàn có thể sử dụng một trong những chiêu thức sau :

• Phương pháp hình học :

Dựa vào mối quan hệ giữa VTCP của đường thẳng và VTPT của mặt phẳng .

• Phương pháp đại số :

Dựa vào số nghiệm của hệ phương trình đường thẳng và mặt phẳng .

3.6.3. Vị trí tương đối giữa đường thẳng và mặt cầu

Để xét VTTĐ giữa đường thẳng và mặt cầu ta hoàn toàn có thể sử dụng những giải pháp sau :

• Phương pháp hình học :

Dựa vào khoảng cách từ tâm mặt cầu đến đường thẳng và nửa đường kính .

• Phương pháp đại số :

Dựa vào số nghiệm của hệ phương trình đường thẳng và mặt cầu .

3.7.1. Khoảng cách từ điểm $M$ đến đường thẳng $d$

• Cách 1 :

Cho đường thẳng USD d USD đi qua $ { { M } _ { 0 } } $ và có VTCP $ \ overrightarrow { a } $ thì USD d \ left ( M, \ d \ right ) = \ frac { \ left | \ left [ \ overrightarrow { { { M } _ { 0 } } M }, \ \ overrightarrow { a } \ right ] \ right | } { \ left | \ overrightarrow { a } \ right | } $

• Cách 2 :

• Tìm hình chiếu vuông góc $ H $ của USD M $ trên đường thẳng USD d USD

• USD d \ left ( M, d \ right ) = MH $

• Cách 3 :

• Gọi $ N \ left ( x, y, z \ right ) \ in d USD

  . Tính USD M { { N } ^ { 2 } } $ theo $ t \ ( t USD

  tham số trong phương trình đường thẳng USD d ) USD

• Tìm USD t $ để USD M { { N } ^ { 2 } } $ nhỏ nhất .

• Khi đó $ N \ equiv H. $ Do đó USD d \ left ( M, \ d \ right ) = MH. $

3.7.2. Khoảng cách giữa hai đường thẳng chéo nhau

Cho hai đường thẳng chéo nhau $ { { d } _ { 1 } } $ và $ { { d } _ { 2 } }. $ Biết $ { { d } _ { 1 } } $ đi qua điểm $ { { M } _ { 1 } } $ và có VTCP $ { { \ overrightarrow { a } } _ { 1 } }, \ { { d } _ { 2 } } $ đi qua điểm $ { { M } _ { 2 } } $ và có VTCP $ \ overrightarrow { { { a } _ { 2 } } } $ thì USD d \ left ( { { d } _ { 1 } }, { { d } _ { 2 } } \ right ) = \ frac { \ left | \ left [ { { \ overrightarrow { a } } _ { 1 } }, { { \ overrightarrow { a } } _ { 2 } } \ right ]. \ overrightarrow { { { M } _ { 1 } } { { M } _ { 2 } } } \ right | } { \ left | \ left [ { { \ overrightarrow { a } } _ { 1 } }, { { \ overrightarrow { a } } _ { 2 } } \ right ] \ right | } $

Chú ý:

Khoảng cách giữa hai đường thẳng chéo nhau $ { { d } _ { 1 } }, \ { { d } _ { 2 } } $ bằng khoảng cách giữa $ { { d } _ { 1 } } $ với mặt phẳng $ \ left ( \ alpha \ right ) USD chứa $ { { d } _ { 2 } } $ và song song với $ { { d } _ { 1 } }. $

3.7.3. Khoảng cách giữa hai đường thẳng song song

Khoảng cách giữa hai đường thẳng song song bằng khoảng cách từ một điểm thuộc đường thẳng này đến đường thẳng kia .

3.7.4. Khoảng cách giữa một đường thẳng và một mặt phẳng song song

Khoảng cách giữa đường thẳng với mặt phẳng $\left( \alpha  \right)$ song song với nó bằng khoảng cách từ một điểm M  bất kì trên d đến mặt phẳng $\left( \alpha  \right)$.

3.8.1. Góc giữa hai đường thẳng

Cho hai đường thẳng $ { { d } _ { 1 } }, \ { { d } _ { 2 } } $ lần lượt có những VTCP $ { { \ overrightarrow { a } } _ { 1 } }, \ { { \ overrightarrow { a } } _ { 2 } } $ .
Góc giữa $ { { d } _ { 1 } }, \ { { d } _ { 2 } } $ bằng hoặc bù với góc giữa $ { { \ overrightarrow { a } } _ { 1 } }, \ { { \ overrightarrow { a } } _ { 2 } } $ là : $ \ cos \ left ( { { \ overrightarrow { a } } _ { 1 } }, { { \ overrightarrow { a } } _ { 2 } } \ right ) = \ frac { \ left | { { \ overrightarrow { a } } _ { 1 } }. { { \ overrightarrow { a } } _ { 2 } } \ right | } { \ left | { { \ overrightarrow { a } } _ { 1 } } \ right |. \ left | { { \ overrightarrow { a } } _ { 2 } } \ right | } $

3.8.2. Góc giữa một đường thẳng và một mặt phẳng

Cho đường thẳng USD d USD có VTCP $ \ overrightarrow { a } = \ left ( { { a } _ { 1 } }, { { a } _ { 2 } }, { { a } _ { 3 } } \ right ) USD và mặt phẳng $ \ left ( \ alpha \ right ) USD có VTPT $ \ overrightarrow { n } = \ left ( A, B, C \ right ) USD .
Góc giữa đường thẳng USD d USD và mặt phẳng $ \ left ( \ alpha \ right ) USD bằng góc giữa đường thẳng USD d USD với hình chiếu USD d $ ’ của nó trên $ \ left ( \ alpha \ right ) USD là : $ \ sin \ left ( \ widehat { d, \ left ( \ alpha \ right ) } \ right ) = \ frac { \ left | A { { a } _ { 1 } } + B { { a } _ { 2 } } + C { { a } _ { 3 } } \ right | } { \ sqrt { { { A } ^ { 2 } } + { { B } ^ { 2 } } + { { C } ^ { 2 } } } \ sqrt { { { a } _ { 1 } } ^ { 2 } + { { a } _ { 2 } } ^ { 2 } + { { a } _ { 3 } } ^ { 2 } } } $

4.1.1. Phương trình chính tắc

 4.1.2. Phương trình tổng quát

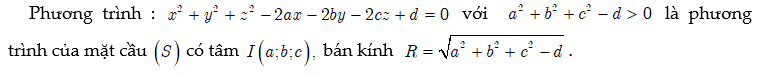
4.3. Một số bài toán tương quan

4.3.1. Dạng 1

$ \ left ( S \ right ) USD có tâm USD I \ left ( a, b, c \ right ) USD và nửa đường kính $ R $ thì $ \ left ( S \ right ) = { { \ left ( x-a \ right ) } ^ { 2 } } + { { \ left ( y-b \ right ) } ^ { 2 } } + { { \ left ( z-c \ right ) } ^ { 2 } } = { { R } ^ { 2 } } $

4.3.2. Dạng 2

$ \ left ( S \ right ) USD có tâm USD I \ left ( a, b, c \ right ) USD và đi qua điểm $ A $ thì nửa đường kính USD R = IA $ .

4.3.3. Dạng 3

$ \ left ( S \ right ) USD nhận đoạn thẳng $ AB $ cho trước làm đường kính :

• Tâm USD I $ là trung điểm của đoạn thẳng

USD AB : \ { { x } _ { 1 } } = \ frac { { { x } _ { A } } + { { x } _ { B } } } { 2 } ; \ { { y } _ { 1 } } = \ frac { { { y } _ { A } } + { { y } _ { B } } } { 2 } ; \ { { z } _ { 1 } } = \ frac { { { z } _ { A } } + { { z } _ { B } } } { 2 } $

• Bán kính USD R = IA = \ frac { AB } { 2 } $

4.3.4. Dạng 4

$ \ left ( S \ right ) USD đi qua bốn điểm $ A, B, C, D $ ( mặt cầu ngoại tiếp tứ diện )

• Giả sử phương trình mặt cầu $ \ left ( S \ right ) USD có dạng :

USD { { x } ^ { 2 } } + { { y } ^ { 2 } } + { { z } ^ { 2 } } + 2 ax + 2 by + 2 cz + d = 0 \ \ left ( * \ right ) USD

• Thay lần lượt toạ độ của những điểm $ A, B, C, D $ vào ( * ) ta được 4 phương trình .

• Giải hệ phương trình đó, ta tìm được $ a, \ b, \ c, d \ \ Rightarrow $ Phương trình mặt cầu $ \ left ( S \ right ) USD .

4.3.5. Dạng 5

$ \ left ( S \ right ) USD đi qua ba điểm $ A, \ B, \ C $ và có tâm USD I $ nằm trên mặt phẳng $ \ left ( P \ right ) USD cho trước thì giải tương tự dạng 4

4.3.6. Dạng 6

$ \ left ( S \ right ) USD có tâm USD I $ và tiếp xúc với mặt cầu $ \ left ( T \ right ) USD cho trước :

• Xác định tâm I và bán kính R’

   của mặt cầu ( T )

  .

• Sử dụng điều kiện kèm theo tiếp xúc của hai mặt cầu để tính nửa đường kính $ R $ của mặt cầu $ \ left ( S \ right ) USD. ( Xét hai trường hợp tiếp xúc trong và ngoài )

Chú ý:

4.3.7. Dạng 7

Viết phương trình mặt cầu ( S ) có tâm I ( a, b, c ), tiếp xúc với mặt phẳng ( P. ) cho trước thì nửa đường kính mặt cầu R = d ( I ; ( P. ) )

4.3.8. Dạng 8

Viết phương trình mặt cầu ( S ) có tâm I ( a, b, c ), cắt mặt phẳng ( P. ) cho trước theo giao tuyến là một đường tròn thoả điều kiện kèm theo .

• Đường tròn cho trước ( nửa đường kính hoặc diện tích quy hoạnh hoặc chu vi ) thì từ công thức diện tích quy hoạnh đường tròn $ S = \ pi { { r } ^ { 2 } } $ hoặc chu vi đường tròn $ P = 2 \ pi r USD ta tìm được nửa đường kính đường tròn giao tuyến USD r USD .

• Tính USD d = d \ left ( I, \ left ( P \ right ) \ right ) USD

• Tính nửa đường kính mặt cầu $ R = \ sqrt { { { d } ^ { 2 } } + { { r } ^ { 2 } } } $

• Kết luận phương trình mặt cầu .

4.3.9. Dạng 9

Viết phương trình mặt cầu ( S ) tiếp xúc với một đường thẳng $ \ Delta $ cho trước và có tâm I ( a, b, c ) cho trước thì đường thẳng $ \ Delta $ tiếp xúc với mặt cầu ( S ) ta có R = d ( I ; $ \ Delta $ ) .

4.3.10. Dạng 10

4.3.10. Dạng 10

4.3.11. Dạng 11

Tập hợp điểm là mặt cầu. Giả sử tìm tập hợp điểm USD M $ thoả đặc thù $ \ left ( P \ right ) USD nào đó .

• Tìm hệ thức giữa những toạ độ USD x, \ y, z USD của điểm USD M USD

USD { { \ left ( x-a \ right ) } ^ { 2 } } + { { \ left ( y-b \ right ) } ^ { 2 } } + { { \ left ( z-c \ right ) } ^ { 2 } } = { { R } ^ { 2 } } $ hoặc : $ { { x } ^ { 2 } } + { { y } ^ { 2 } } + { { z } ^ { 2 } } + 2 ax + 2 by + 2 cz + d = 0 USD

• Tìm số lượng giới hạn quĩ tích ( nếu có ) .

4.3.12. Dạng 12

Tìm tập hợp tâm mặt cầu

• Tìm toạ độ của tâm $I$, chẳng hạn: $\left\{ \begin{array}{l}
  x = f\left( t \right)\\
  y = g\left( t \right)\\
  z = h\left( t \right)
  \end{array} \right.$

• Khử USD t $ trong ( * ) ta có phương trình tập hợp điểm .

• Tìm số lượng giới hạn quĩ tích ( nếu có ) .

Cho $ \ left ( P \ right ) USD và hai điểm $ A, B. USD Tìm USD M \ in \ left ( P \ right ) USD để $ { { \ left ( MA + MB \ right ) } _ { \ min } } $ ?

Phương pháp

• Nếu $ A $ và $ B $ trái phía so với $ \ left ( P \ right ) \ Rightarrow M, \ A, \ B $

  thẳng hàng $ \ Rightarrow M = AB \ cap \ left ( P \ right ) USD

• Nếu $ A $ và $ B $ cùng phía so với $ \ left ( P \ right ) USD

  thì tìm $ B ‘ $ là đối xứng của $ B $

  qua $ \ left ( P \ right ) USD

Cho $ \ left ( P \ right ) USD và hai điểm $ A, B. USD Tìm USD M \ in \ left ( P \ right ) USD để $ { { \ left | MA-MB \ right | } _ { \ max } } $ ?

Phương pháp

• Nếu $ A $ và $ B $

  cùng

  phía so với $ \ left ( P \ right ) \ Rightarrow M, \ A, \ B $

  thẳng hàng

  USD \ Rightarrow M = AB \ cap \ left ( P \ right ) USD

• Nếu $ A $ và $ B $ trái phía so với $ \ left ( P \ right ) USD thì tìm $ B ‘ $

  là đối xứng của $ B $ qua $ \ left ( P \ right ) USD

USD \ Rightarrow \ left | MA-MB ‘ \ right | = AB ‘ $
Cho điểm USD M \ left ( { { x } _ { M } }, { { y } _ { M } }, { { z } _ { M } } \ right ) USD không thuộc những trục và mặt phẳng tọa độ. Viết phương trình $ \ left ( P \ right ) USD qua USD M $ và cắt 3 tia $ Ox, \ Oy, \ Oz $ lần lượt tại $ A, \ B, \ C $ sao cho USD { { V } _ { O.ABC } } $ nhỏ nhất ?

Phương pháp                       $\left( P \right):\frac{x}{3{{x}_{M}}}+\frac{y}{3{{y}_{M}}}+\frac{z}{3{{z}_{M}}}=1$

Viết phương trình mặt phẳng $ \ left ( P \ right ) USD chứa đường thẳng USD d USD, sao cho khoảng cách từ điểm USD M \ not { \ in } d USD đến $ \ left ( P \ right ) USD là lớn nhất ?

Phương pháp                      $\left( P \right):\left\{ \begin{array}{l}
Qua\;A \in d\\
{\overrightarrow n _{\left( P \right)}} = \left[ {\left[ {{{\overrightarrow u }_d},\overrightarrow {AM} } \right],{{\overrightarrow u }_d}} \right]
\end{array} \right.$

Viết phương trình mặt phẳng $ \ left ( P \ right ) USD qua $ A $ và cách USD M $ một khảng lớn nhất ?

Phương pháp                      $\left( P \right):\left\{ \begin{array}{l}
Qua\;A\\
{\overrightarrow n _{\left( P \right)}} = \overrightarrow {AM} 
\end{array} \right.$

Viết phương trình mặt phẳng $ \ left ( P \ right ) USD chứa đường thẳng USD d USD, sao cho $ \ left ( P \ right ) USD tạo với $ \ Delta $ ( $ \ Delta $ không song song với USD d USD ) một góc lớn nhất là lớn nhất ?

Phương pháp                      $\left( P \right):\left\{ \begin{array}{l}
Qua\;A \in d\\
{\overrightarrow n _{\left( P \right)}} = \left[ {\left[ {{{\overrightarrow u }_d},\overrightarrow {AM} } \right],{{\overrightarrow u }_d}} \right]
\end{array} \right.$

Cho $ \ Delta / / \ left ( P \ right ) USD. Viết phương trình đường thẳng USD d USD nằm trong $ \ left ( P \ right ) USD song song với $ \ Delta $ và cách $ \ Delta $ một khoảng chừng nhỏ nhất ?

Phương pháp

Lấy $A\in \Delta $  , gọi $A’$  là hình chiếu vuông góc của $A$ trên $\left( P \right)$ thì $d:\left\{ \begin{array}{l}
Qua\;A’\\
{\overrightarrow u _d} = {\overrightarrow u _\Delta }
\end{array} \right.$

Viết phương trình đường thẳng USD d USD đi qua điểm $ A $ cho trước và nằm trong mặt phẳng $ \ left ( P \ right ) USD cho trước sao cho khoảng cách từ điểm USD M $ cho trước đến USD d USD là lớn nhất ( $ AM $ không vuông góc với $ \ left ( P \ right ) USD ?

Phương pháp                      $d:\left\{ \begin{array}{l}
Qua\;A \in d\\
{\overrightarrow u _d} = \left[ {{{\overrightarrow n }_{\left( P \right)}},\overrightarrow {AM} } \right]
\end{array} \right.$

Viết phương trình đường thẳng USD d USD đi qua điểm $ A $ cho trước và nằm trong mặt phẳng $ \ left ( P \ right ) USD cho trước sao cho khoảng cách từ điểm USD M $ cho trước đến USD d USD là nhỏ nhất ( $ AM $ không vuông góc với $ \ left ( P \ right ) USD ?

Phương pháp                      $d:\;\left\{ \begin{array}{l}
Qua\;A \in d\\
{\overrightarrow u _d} = \left[ {\left[ {{{\overrightarrow n }_{\left( P \right)}},\overrightarrow {AM} } \right],{{\overrightarrow n }_{\left( P \right)}}} \right]
\end{array} \right.$

Viết phương trình đường thẳng USD d USD đi qua điểm $ A \ in \ left ( P \ right ) USD cho trước, sao cho USD d USD nằm trong $ \ left ( P \ right ) USD và tạo với đường thẳng $ \ Delta $ một góc nhỏ nhất ( $ \ Delta $ cắt nhưng không vuông góc với $ \ left ( P \ right ) USD ) ?

Phương pháp

 $d:\;\left\{ \begin{array}{l}
Qua\;A \in d\\
{\overrightarrow u _d} = \left[ {\left[ {{{\overrightarrow n }_{\left( P \right)}},\overrightarrow {AM} } \right],{{\overrightarrow n }_{\left( P \right)}}} \right]
\end{array} \right.$

Source: https://vh2.com.vn
Category : Trái Đất