Cách chứng minh tam giác vuông. | Chuyên đề toán | BaiTap.me

Bạn nhìn nhận : ChưaTrong phân môn hình học của chương trình toán trung học phổ thông ta thường gặp một số ít dạng toán quen thuộc như chứng minh một tam giác nào đó là vuông, cân hoặc đều. Chuyên đề này nhằm mục đích xử lý khó khăn vất vả cho những em học viên khi gặp phải bài toán chứng minh một tam giác vuông .

Tam giác vuông là gì ?

Tam giác vuông là một tam giác có một góc là góc vuông (góc 90 độ). Mối quan hệ giữa các cạnh và góc của một tam giác vuông là nền tảng cơ bản của lượng giác học.

Một số cách chứng minh tam giác vuông thường gặp

Cho  có 

1. Chứng minh tam giác vuông bằng cách chỉ ra tam giác có một góc bằng 

Phương pháp :

• Để chỉ ra tam giác có một góc bằng  ta cần biến đổi giả thiết về các dạng như từ đó suy ra tam giác  vuông tại 

Lưu ý : Các công thức lượng giác hay sử dụng là

• Công thức cộng : 

• Công thức nhân đôi, hạ bậc : 

• Công thức biến đổi tổng thành tích, tích thành tổng: 

• Các hệ thức lượng trong tam giác : 

Định lý côsin :	Định lý sin :

Ví dụ minh họa : 

Ví dụ 1. Cho tam giác  nhọn thỏa . Chứng minh rằng  vuông.

Lời giải :  

Ta có 

Vì tam giác  nhọn nên , do đó 

Ví dụ 2. Cho tam giác  thỏa .

Lời giải :  

Theo định lý sin ta có :  nên 

Vậy tam giác  vuông tại 

Chú ý : 

• Nếu  thì  vuông tại 
• Nếu  thì  vuông tại 
• Nếu  thì  vuông tại 

Ví dụ 3. Cho tam giác  thỏa mãn  và   Chứng minh tam giác  vuông.

Lời giải : 

Theo định lý sin ta có :  

Vì  nên ,do đó 

Vậy tam giác vuông tại 

2. Chứng minh tam giác vuông bằng cách sử dụng định lý Pi-ta-go. 

Phương pháp : Vận dụng định lý pi-ta-go cho tam giác vuông bằng cách đưa giả thiết bài toán về một trong các trường hợp sau

• Nếu  thì   vuông tại 
• Nếu  thì  vuông tại 
• Nếu  thì  vuông tại 

Ví dụ minh họa : 

Ví dụ 1.  có tính chất gì nếu độ dài ba cạnh lần lượt là .

Lời giải : 

Dễ nhận thấy rằng  Do đó tam giác  vuông tại .

Ví dụ 2. Cho  thỏa , chứng minh rằng  vuông.

Lời giải : 

Theo hệ thức lượng trong tam giác ta có  nên 

Vậy  vuông tại 

Ví dụ 3 : Cho  thỏa  , chứng minh rằng  vuông.

Lời giải : 

Ta có 

Vậy  vuông tại 

3. Chứng minh tam giác vuông dựa vào tích vô hướng của hai vectơ.

Phương pháp :  

  vuông tại  khi  hay  Như vậy ta có thể đưa bài toán chứng minh một tam giác vuông trở thành bài toán tính cá tích vô hướng. Ta có các trường hợp sau

• Để chứng minh  vuông tại  ta có thể chứng minh 
• Để chứng minh  vuông tại  ta có thể chứng minh 
• Để chứng minh  vuông tại  ta có thể chứng minh 

Chú ý : Các công thức hay sử dụng

•  (định nghĩa tích vô hướng)
•  (biểu thức tọa độ của tích vô hướng)
• 

Ví dụ minh họa : 

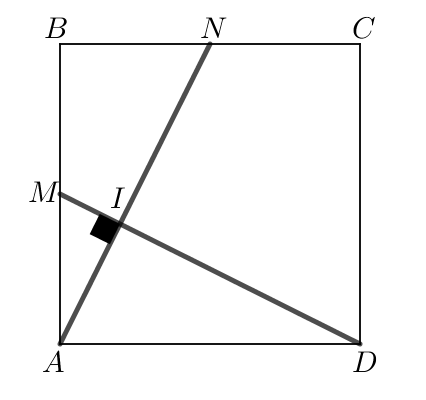
Ví dụ 1. Cho hình vuông  lần lượt là trung điểm . Gọi . Chứng minh rằng vuông.

Phân tích : Dự đoán rằng  vuông tại  nên ta có thể chứng minh  dựa vào định nghĩa tích vô hướng.

Lời giải : 

Để chứng minh tam giác  vuông ta có thể chứng minh 

Thật vậy, ta có 

Mặt khác :

•   
• 
• 

Vậy  vuông tại  

Ví dụ 2. Trong mặt phẳng tọa độ, cho tam giác  có . Chứng minh rằng tam giác  vuông.

Phân tích : Dễ thấy rằng đây là dạng toán có gắn tọa độ nên ta chỉ việc áp dụng biểu thức tọa độ của tích vô hướng. 

Lời giải : 

Ta có   vuông tại 

Ví dụ 3. Trong mặt phẳng tọa độ, cho . Tìm tọa độ điểm  trên trục hoành sao cho tam giác  vuông tại 

Lời giải : 

Vì  nằm trên trục hoành nên tọa độ có dạng  Khi đó ta có  : 

Kết luận : Khi gặp bài toán chứng minh tính vuông góc, trước hết ta cần phân biệt các dạng toán, nếu dạng toán liên quan đến các đẳng thức lượng giác thì ta nên vận dụng các công thức lượng giác và các hệ thức lượng trong tam giác. Nếu bài toán thuộc dạng hình học thuần túy hay có gắn tọa độ thì sử dụng tích vô hướng để giải quyết.

Source: https://vh2.com.vn
Category : Trái Đất