Đồ họa của Tech Insider cho thấy những lục địa sẽ hợp nhất thành một dải đất duy nhất trong vòng 250 triệu năm tới . Bạn đang đọc: Các...
Cách vẽ hình học không gian lớp 11 chuẩn nhất
1. Nắm bắt nguyên tắc cơ bản về vẽ hình trong hình học không gian
Hình vẽ là yếu tố cơ bản phân định hình học không gian so với những dạng toán khác của Toán học. Muốn học tốt hình học không gian thì việc thứ nhất phải làm đó là nắm vững nguyên tắc cơ bản về vẽ hình. Phương pháp vẽ hình dưới đây sẽ giúp bạn có cái nhìn dễ hơn và tưởng tượng tốt hơn khi tìm phương pháp giải bài. – Khi đọc đề điều tiên phong cần xác lập là vẽ cái gì trước cái gì sau. Bạn cần vẽ mặt phẳng được cho trước nằm ngang theo dạng hình bình hành, phần mặt dưới vừa phải không hẹp quá cũng không rộng quá tránh khó thêm chi tiết cụ thể về sau.
– Lưu ý những đường ẩn bị che khuất phải vẽ bằng nét đứt và những đường nhìn thấy sẽ là nét liền. Điều này rất quan trọng quyết định hình vẽ của bạn đúng hay sai.
Bạn đang đọc: Cách vẽ hình học không gian lớp 11 chuẩn nhất
– Đối với những đường song song cần nhu yếu vẽ chuẩn xác tránh việc vẽ lệch dẫn đến nhìn sai và không tìm được manh mối xử lý bài toán. – Nếu như đường tròn là mặt dưới thì vẽ hình elip không quá to tránh việc khó vẽ những cạnh còn lại và không quá hẹp để tránh rối mắt khi vẽ thêm những đường khác. Còn dưới mặt đáy là hình vuông vắn hay hình chữ nhật hoặc hình thoi thì khi vẽ trong hình học không gian đều sẽ là hình bình hành. Đặc biệt với dưới mặt đáy là hình thang thì phải vẽ nghiêng về một bên cho dễ nhìn hình dễ tưởng tượng.
.jpg)
– Không được bỏ lỡ những ký hiệu góc đặc biệt quan trọng là góc vuông để tránh bỏ lỡ liên hệ góc khi giải bài. – Đường thẳng vuông góc là phải đường thẳng được vẽ chuẩn nhất, theo hướng vuông góc. Tránh kẻ lệch và cong vì sẽ khiến biến hóa độ của góc. – Những đường thẳng khi cắt nhau thì nên vẽ sang trái hoặc phải, hạn chế vẽ về phía sau dễ bị rối mắt khó nhìn hình. Một số bước quan tâm vẽ hình phía trên cho thấy tầm quan trọng của việc vẽ hình trong giải bài toán hình học không gian. Chỉ cần vẽ sai hoặc sẽ không thuận mắt là bạn đã gặp phải rắc rối trong việc giải bài. Khi đọc đề bạn cần tìm ra được những bước xử lý theo thứ tự và vẽ hình theo từng bước giải, tránh việc vẽ trước hết sẽ gây khó nhìn, nhìn sai làm bài toán rẽ sang hướng khác.
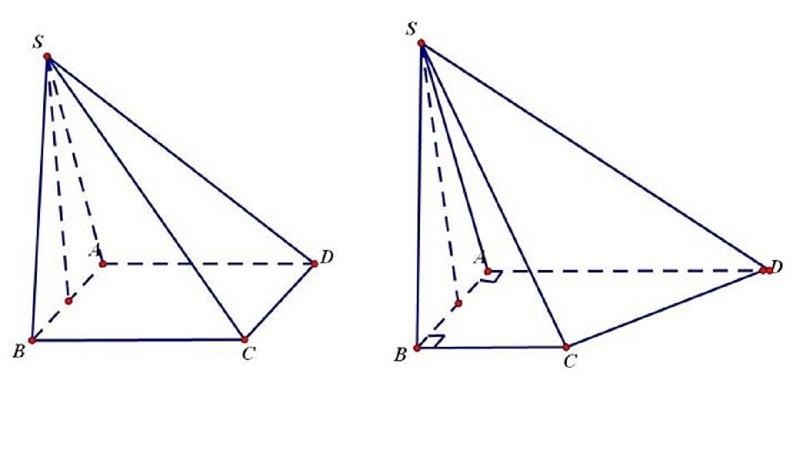
Đối với hình học bạn hoàn toàn có thể vẽ bằng bút chì để thuận tiện tẩy xóa, tuy nhiên vẫn nên vẽ ra giấy nháp trước để không làm bẩn bài và tránh mất thời hạn cho việc chỉnh sửa. Hình học có thích mắt có dễ nhìn mới nhanh gọn tìm được cách giải và đáp án đúng. Muốn giải được toán hình phải đi ngược lại những hướng xuất phát từ những điểm đã cho. Hình học không gian nhu yếu bạn phải ghi nhớ và có cái nhìn logic để vận dụng những công thức, định lý vào giải bài.
2. Các bước cần ghi nhớ để làm tốt bài tập về hình học không gian
2.1. Phân tích và chọn ra mấu chốt yếu tố cần xử lý
Trước khi đến với hình học không gian bạn sẽ được tập làm quen với hình học phẳng để chớp lấy được cách xử lý yếu tố trên từng mặt của khối đa diện trong hình học không gian. Bước chuyển giao giữa hình học phẳng và hình học không gian sẽ khiến nhiều bạn kinh ngạc và cảm thấy khó khăn vất vả trong việc tiếp thu. Đặc biệt là với những bạn tưởng tượng không được tốt sẽ khó tìm thấy sự liên hệ giữa góc cạnh và vẽ hình. Đó là nguyên do hình học không gian nhu yếu bạn làm tốt bước vẽ hình để rèn luyện trí tưởng tượng. Ngoài việc phải tưởng tượng tốt thì nên chọn cách liên tưởng để dễ tưởng tượng về đề bài. Ví dụ bài cho hình hộp thì tìm kiếm những đồ vật quen thuộc có hình hộp như hộp giấy, bao diêm, … đề cho hình lập phương thì hoàn toàn có thể liên tưởng đến khối rubik, … Hình học không gian đã cho bạn rất nhiều ví dụ từ chính cái tên của nó như không gian lớp học, phòng nghỉ hay cần mối liên hệ về góc cạnh hoàn toàn có thể tìm đến góc bàn, góc bác, góc tạo thành từ chân bàn với mặt bàn, sàn nhà với tường nhà, … có rất nhiều thứ bạn hoàn toàn có thể liên hệ để sử dụng cho giải bài toán về hình học không gian.

2.2. Chú ý quan sát và nghiên cứu và phân tích đề khi phát hiện hình học không gian
Khi đọc đề cần chú ý quan tâm đừng khi nào chỉ vẽ hình một lần, hãy vẽ đến khi bạn nhìn ra được yếu tố và tìm được hướng xử lý. Tránh mặt khuất ra và vẽ sao cho mọi yếu tố được hiển thị rõ nhất ở mặt bên và mặt dưới. Góc nhìn cũng cần rất là linh động và đổi khác liên tục để không bỏ sót chi tiết cụ thể nào giúp tìm ra giải thuật. Trong đề bài những cụ thể cho trước thường ngắn gọn nhưng rất đáng giá. Ví dụ như đề cho một hình chóp đều cạnh a là bạn đã hoàn toàn có thể liên hệ đến rất nhiều kỹ năng và kiến thức tương quan như những cạnh bằng nhau, những mặt bên bằng nhau, góc hợp bởi cạnh bên với đáy bằng nhau, … Tổng hợp lại tổng thể những thông tin đề cho, suy ngược lại từ những điểm đó. Ví dụ đề nhu yếu chứng tỏ hai mặt phẳng vuông góc với nhau thì tìm kiếm mọi tài liệu, công thức tương quan đến góc vuông, hai đường thẳng vuông góc, hai mặt phẳng song song, …
2.3 .Ghi nhớ kỹ năng và kiến thức cơ bản cần nắm rõ trong hình học không gian
Mọi kỹ năng và kiến thức trong hình học không gian đều có mối liên hệ ngặt nghèo với nhau nên việc liên hệ để nhớ ra công thức cần vận dụng không khó. Ví dụ đề nhu yếu chứng tỏ mặt phẳng vuông góc với mặt phẳng, thì hướng đi tiên phong sẽ là đưa về chứng tỏ đường thẳng với mặt phẳng, để chứng tỏ đường thẳng vuông góc với mặt phẳng thì cần chứng tỏ đường thẳng đó vuông góc với hai đường thẳng thuộc mặt phẳng đó. Việc này buộc bạn phải lật lại những kỹ năng và kiến thức trước đó vì những điều cơ bản học tiên phong sẽ sử dụng để chứng tỏ những yếu tố về mặt phẳng rồi mới đến hình học không gian.

Để khi nhớ những kiến thức và kỹ năng này bạn hoàn toàn có thể tự tạo sơ đồ tư duy cho bản thân. Mỗi chiêu thức, định lý nên có hình vẽ minh họa theo cùng. Sơ đồ này không chỉ giúp bạn thuận tiện mạng lưới hệ thống kiến thức và kỹ năng mà còn kích thích trí tưởng tượng và tăng cường năng lực ghi nhớ của bạn. Bạn hoàn toàn có thể tự tạo sổ tay mang theo hoặc liên hệ kỹ năng và kiến thức đến chính những vật phẩm và không gian xung quanh mình từ nhìn những hình chóp ở mái nhà, hình hộp ở những đồ vật hay chính ngôi nhà bạn ở, …
3. Mẹo xử lý những dạng đề trong hình học không gian
3.1. Dạng bài tìm giao tuyến của hai mặt phẳng
Dạng bài này sẽ có 2 cách cho bạn lựa chọn để giải bài tập : Cách 1 : Bạn sẽ phải tìm ra 2 điểm chung của 2 mặt phẳng đó – Điểm chung thứ nhất thường biểu lộ ngay trên hình vẽ và sẽ không làm khó bạn.
– Giao điểm của hai đường thẳng còn lại sẽ là điểm chung thứ 2 và không đi qua trung điểm thứ nhất.
Xem thêm: Những bức ảnh về ‘Trái đất xưa và nay’: Trái đất đã thay đổi như thế nào trong hơn 100 năm qua?
Cách 2 : Trong 2 mặt phẳng mà có chứa 2 đường thẳng song song thì bạn chỉ cần tìm 1 điểm chung, giao tuyến sẽ đi qua điểm chung đó và song song với 2 đường thẳng này.
3.2. Dạng bài tìm giao điểm của đường thẳng a và mặt phẳng ( P. )
– Bạn cần lấy ra một đường thẳng b thuộc mặt phẳng ( P. ) và tìm giao điểm của đường thẳng a với đường thẳng b. – Nếu không có đường thẳng b thì cần tìm một mặt phẳng ( Q. ) có chứa đường thẳng a. Ta tìm giao tuyến b của mặt phẳng ( P. ) và mặt phẳng ( Q. ). Sau đó gọi A = a ∩ b thì A = a ∩ ( P. ).

3.3. Dạng bài chứng tỏ 3 điểm thẳng hàng
Đây là một dạng đề khó yên cầu những bạn phải tư duy khá nhiều. Đối với việc chứng tỏ 3 điểm hay nhiều hơn 3 điểm thẳng hàng thì bạn cần phải chứng tỏ được chúng thuộc 2 mặt phẳng phân biệt không cắt nhau.
3.4. Dạng bài chứng tỏ 3 đường thẳng a, b, c đồng quy khá phổ cập và dễ gây rối
Dạng bài này cũng cho bạn 2 cách làm bài để bạn lựa chọn theo hướng tư duy tương thích với bản thân : Cách 1 : Bạn sẽ phải chứng tỏ giao điểm của 2 đường thẳng này là điểm chung của 2 mặt phẳng mà giao tuyến là đường thẳng thứ 3 để thấy được điểm liên hệ cần chứng tỏ. Ví dụ : Tìm A = a ∩ b, ta phải tìm 2 mặt phẳng ( P. ), ( Q. ) chứa A mà ( Q. ) ∩ ( P. ) = c, đây là một ví dụ cơ bản tuy nhiên vào đề bạn sẽ phải quan tâm nhiều hơn vì sẽ có tính mẹo để đánh lạc hướng. Cách 2 : Chứng minh a, b, c không cùng nằm trên một mặt phẳng và cắt nhau từng đôi một
3.5. Dạng bài tìm điểm M gồm có những tập hợp giao điểm của 2 đường thẳng di động a, b
– Trước tiên tìm a thuộc mặt phẳng cố định và thắt chặt nào. – Sau đó tìm mặt phẳng ( Q. ) cố định và thắt chặt chứa b. – Ta có : c = ( P. ) ∩ ( Q. ), được M thuộc c. – Cuối cùng là số lượng giới hạn.
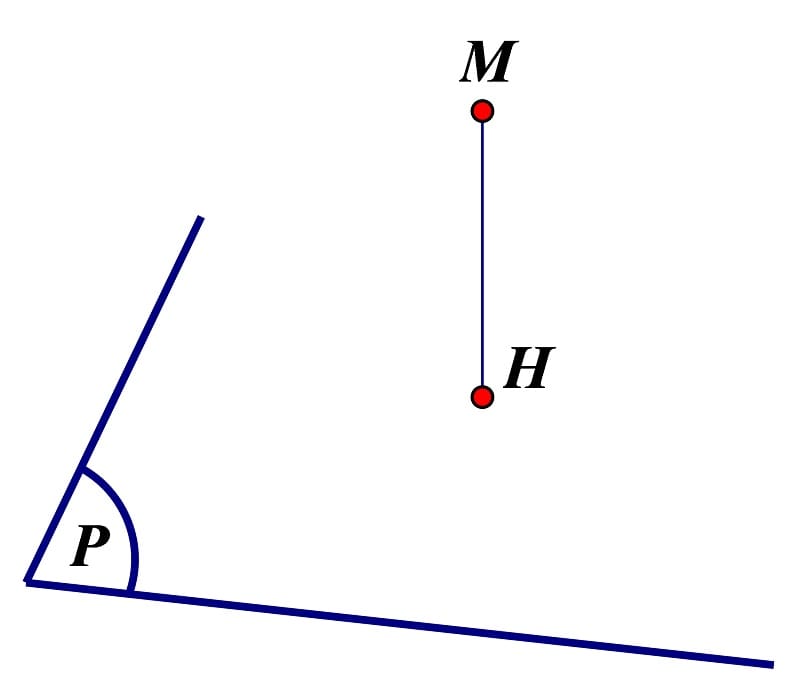
3.6. Dạng bài dựng thiết diện của mặt phẳng ( P. ) và một khối đa diện T .
Muốn làm được dạng đề này bạn cần phải tìm giao tuyến của mặt phẳng ( P. ) với những mặt của T. Các bước sau đây sẽ giúp bạn xử lý bài toán hình học không gian này thuận tiện hơn : – Bắt đầu với những điểm chung có sẵn, ta cần phải xác lập giao tuyến tiên phong của ( P. ) với một mặt của T để hình thành bước tư duy tiên phong. – Tìm giao điểm của giao tuyến với những cạnh của một mặt phẳng cách lê dài giao tuyến đã có. Làm tựa như sẽ ra được những giao tuyến còn lại. Phần khép kín giữa những đoạn giao tuyến chính là thiết diện cần dựng theo nhu yếu của bài toán
4. Nắm bắt được hình và dạng bài hình không gian
Khởi đầu của việc học hình học không gian hoàn toàn có thể sẽ bị cản trở nhiều bởi trí tưởng tượng nhưng điểm yếu này là trọn vẹn hoàn toàn có thể khắc phục bằng cách làm nhiều bài tập và ghi chép công thức, định lý ra sổ tay để ôn tập. Ngoài ra mua thêm cho mình những cuốn sách tìm hiểu thêm cũng là một quan điểm hay giúp cải tổ môn học này. Những cuốn sách bạn chọn nhất định phải có phần tóm tắt kiến thức và kỹ năng của sách giáo khoa đi kèm với ví dụ đơn cử, phần tiếp theo mới là bài tập được phân dạng rõ ràng, có giải thuật dễ hiểu và mạch lạc.
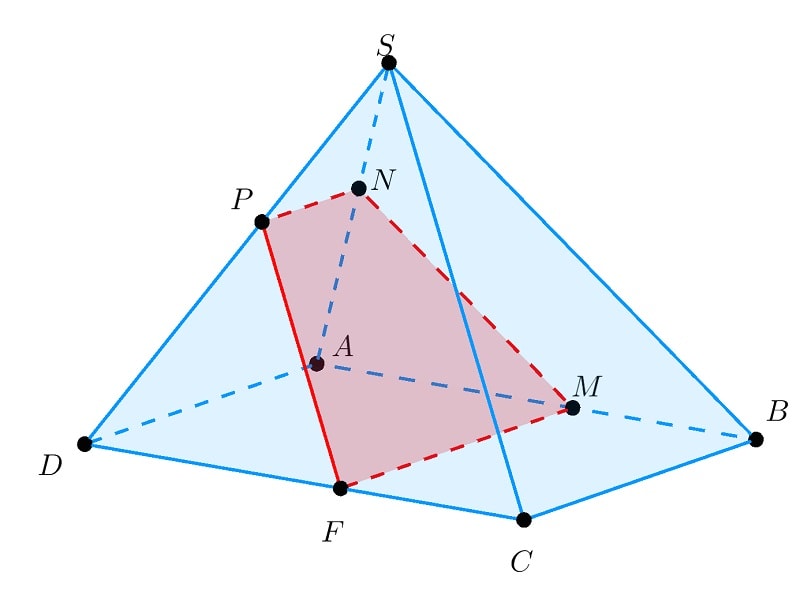
Xem thêm: Keanu Reeves – Wikipedia tiếng Việt
Hình học không gian không được cho phép bạn tư duy một mình mà phải tìm hiểu thêm thêm nhiều lối tư duy và cái nhìn của nhiều người khác nữa. Nên việc xung phong lên bảng giải bài để được thầy cô và những bạn góp ý là điều rất thiết yếu. Xem trước đáp án không phải là xấu và cần phải xem khi không tìm được lời giải để hiểu về những phương pháp khác nhau cho cách giải bài toán này. Từ đó tìm ra cách dễ hiểu nhất, giải lại theo cách tư duy của bạn để biến nó thành giải thuật của bản thân, việc này sẽ cho bạn ấn tượng về bài toán và thuận tiện gợi nhớ lại. Hình học không gian chỉ khó thật sự khi bạn mãi để nó lại với từ khó mà không chịu tìm tòi phương pháp biến hóa tâm lý của bản thân. Những gì bạn cần chỉ là đọc bài viết này và đổi khác tâm lý rồi rèn luyện bản thân. Bạn nên nhớ hình học không gian không số lượng giới hạn tư duy của bất kể ai mà còn cho bạn cái nhìn tinh xảo sắc nét về nhiều góc nhìn của đời sống.
>> Tham khảo thêm:
Source: https://vh2.com.vn
Category : Trái Đất





