[SGK Scan] ✅ Vectơ trong không gian. Sự đồng phẳng của các vectơ – Sách Giáo Khoa – Học Online Cùng https://vh2.com.vn

Xem thêm các sách tham khảo liên quan:

Vectơ trong không gian. Sự đồng phẳng của những vectơ –
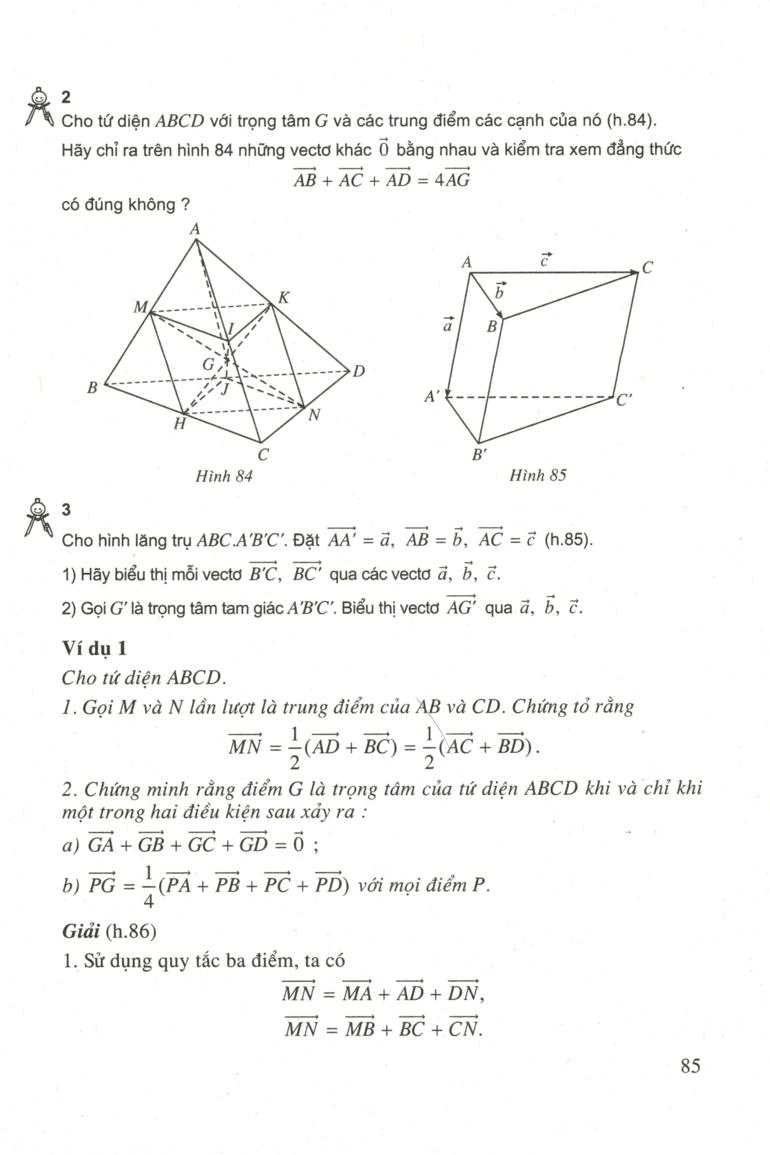
Khái niệm vectơ và những phép toán vectơ đã được đề cập trong chương trình hình học lớp 10. Tuy nhiên, khi đó tổng thể những vectơ mà tất cả chúng ta xem xét đều nằm trên cùng một mặt phẳng. Ở chương II, tất cả chúng ta đã làm quen với việc A điều tra và nghiên cứu hình học không gian mà đối tượng người tiêu dùng của nó là những hình hoàn toàn có thể không cùng nằm trong một mặt phẳng. Chẳng hạn, tứ diện ABCD là một hình có đặc thù đó và như vậy những vectơ AB, BC, CD không cùng nằm trong một mặt phẳng nào cả ( h. 82 ). Trong chương này, tất cả chúng ta sẽ nói đến những vectơ trong không gian. Vectơ, những phép toán C vectơ trong không gian được định nghĩa hoàn Hình 82 toàn giống như trong mặt phẳng, chúng cũng có những đặc thù đã biết nên không nhắc lại. Sau đây, tất cả chúng ta nêu lên 1 số ít hoạt động giải trí và ví dụ nhằm mục đích mục tiêu ôn tập lại những kiến thức và kỹ năng đã có về vectơ trong mặt phẳng để vận dụng vào không gian. 1C ho hình hộp ABCD, A’B ’ C’D ’, với tâm O ( h. 83 ). B a ). Hãy chỉ ra trên hình 83 những vectơ bằngnhau khác vectơ 0 và kiểm tra tính đúng đắn của đẳng thứcAC ” = AB + AD + AA ”. ( 1 ) b ) Chứng minh rằng AB + B’C ’ + DVD = AD + D’Co ’ + B’B = A ’ C.Hình 83CH Ú Ý Công thức ( 1 ) gọi là quy tắc hình hộp ( để tìm tổng của ba vectơ ). 2 汽 Cho tứ diện ABCD với trọng tâm G và những trung điểm những cạnh của nó ( h. 84 ). Hãy chỉ ra trên hình 84 những vectơ khác 0 bằng nhau và kiểm tra xem đẳng thức AB + AC + AD = 4AGA. C A. C. ’ B’C Hình 84 Hình 85 có đúng không ? A. 3 Cho hình lăng trụ ABCA’B ’ C ”. Đặt AA ’ = ā, AB = 5, AC = C ( h. 85 ). 1 ) Hãy bộc lộ mỗi vectơ B °C, BC ” qua những vectơ ä, b, c, 2 ) Gọi G là trọng tâm tam giác A’B ’ C ’, Biểu thị vectơ AG ” qua ä, b, c, Ví dụ 1 Cho tứ diện ABCD. 1. Gọi M và N lần lượt là trung điểm của AB và CD. Chứng tỏ rằng MN = ( AD + BC ) = AC + BD ). 2. Chứng minh rằng điểm G là trọng tâm của tứ diện ABCD khi và chỉ khi một trong hai điều kiện kèm theo sau xảy ra : a ) GA + GB + GC + GD = 0 b ) PG = ( P. + PB + PC + PD ) với mọi điểm P. Gidi ( h. 86 ) 1. Sử dụng quy tắc ba điểm, ta có MN = MA + AD + Doanh Nghiệp, MN = MB + BC + CN. Do MA + MB = 0 và Doanh Nghiệp + CN – Önên MN = } ( AD + BC ). MTương tự như trên, ta có – 1 ہے ۔ یہ B D MN = ( AC + BD ). 2. a ) Ta có N GA + GB = 2GM, – – F / in } và 6 GC + GD = 2GN. Điểm G là trọng tâm của tứ diện ABCD khi và chỉ khi GM + GN = 0 hay 2 ( GM + GN ) = ö. Điều này tương tự với GA + GB + GC + GD = 0. b ) G là trọng tâm của tứ diện ABCD khi và chỉ khiGA + GB + GC + GD = 0. Điều này có nghĩa là với điểm P. bất kỳ, ta cóPA PG PB PG PC PG PD PG 6.hay PG = PA + PB + PC PD ). DVí dụ 2 Cho tứ diện ABCD có AB = c, CD = c ’, AC = b., BD = b ^, BC = a, AD = a ^. Tính góc giữa những vectơ BC và DẢ. Giải. Ta có BCDA = BC ( DC + CA ) = CBCD – CBCA ( CB + CD – BD ) – ( CB + CA ” – AB * ) AB + CD – BD-CA ). Từ đó góc ( BC, DA ) xác lập bởi2 – 2 h2 h, 2 cos ( BC, DA ) = — – CIV. Sự đồng phẳng của những vectơ. Điều kiện để ba vectơ đồng phẳngTa biết rằng, với hai đường thẳng phân biệt cho trước trong không gian, luôn có mặt phẳng song song với hai đường thẳng đó. Nhưng nói chung, không có mặt phẳng song song với ba đường thẳng phân biệt cho trước. Nếu có mặt phẳng như vậy thì ta nói rằng ba vectơ nằm trên ba đường thẳng ấy là đồng phẳng. ĐINH NGHIA Ba vectơ gọi là đồng phẳng nếu những giá của chúng cùng song song với một mặt phẳng. Trên hình 87, giá của ba vectơ α. ã, b, c đều song song với mặt っイphẳng ( P. ) nên ba vectơ ä, b, c đồng phẳng. Nhận xét Từ định nghĩa trên, suy ra : Nếu tavē OA = a, OB = b, OC = c thìHình 87 ba vectơ ä, b, c đồng phẳng khi và chỉ khi bốn điểm O, A, B, C cùng nằm trên một mặt phẳng hay ba đường thẳng OA, OB, OC cùng nằm trong một mặt phẳng. Bài toán 1 Cho tứ diện ABCD. Gọi M và N lần A. lượt là trung điểm của AB và CD. Chứng minh rằng ba vectơ BC, MN, M AD đồng phẳng. 飛 4 ( Để giải bài toán 1 ) O Gọi P. và Q. lần lượt là trung điểm của AC vàBD. Khi đó MPNQ là hình bình hành. Từ C N D đó, hãy suy ra điều phải chứng tỏ ( h. 88 ). Hình 88 Điều kiện để ba vectơ đồng phẳng Từ định nghĩa ba vectơ đồng phẳng và sự khai triển một vectơ theo hai vectơ không cùng phương trong hình học phẳng, tất cả chúng ta hoàn toàn có thể chứng tỏ được định lí sau ( h. 89 ). ĐINH LÍ1Cho ba vectoy di, b. C, trong đó ä và b không cùng phương. Điều kiện cẩn và đủ để ba vectơ ä, b, c đồngphẳng là có những số m, n sao cho ẽ = mã + nb. Hơn nữa, những số m, n là duy nhất. B Hình 895 熾 Chứng minh rằng 1 ) Nếu có mã + nh + pc = 0 và một trong ba số m, n, p khác không thì ba vectơ ä, b, c đồng phẳng ; 2 ) Nếu ä, b, c là ba vectơ không đồng phẳng và mã + nh + pể = Ở thìm = n = p = 0. Bài toán 2 Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Lấy những điểm P., Q. lần lượt thuộc những đường thẳng AD và BC sao cho PẢ = kPD, QB = kQC ( k z 1 ). Chứng minh rằng những điểm M, N, P., Q. cùng thuộc một mặt phẳng ( h. 90 ). 6 ( Để giải bài toán 2 ) C 1 ) Từ hệ thức PA = kPD, hãy chứng tỏ F / inh 90 MP = MA – kMD. 1 一雄 Tương tự, ta cũng cósee MB-kMCMO = T-T -. Ο 1 一从 2 ) Từ hai đẳng thức trên, chứng tỏ rằng MP + MG = MN.Vậy những điểm M, N, P., Q. cùng thuộc một mặt phẳng. Định lí 1 : nói đến điều kiện kèm theo để hoàn toàn có thể biểu lộ một vectơ qua hai vectơ không cùng phương. Định lí dưới đây sẽ nói về biểu lộ một vectơ qua ba vectơ không đồng phẳng. ĐINH LÍ2Nếu ä, b, c là ba vectơ không đồng phẳng thì với mỗi vectơ đi, ta tìm được những sốm, n, p sao cho đ = mã + n5 + pẽ. Hơn nữa, những sốm, n, p là duy nhất. Chứng minh Từ điểm O, ta đặt OA = ä, OB = 5, OC = c, OD = d thì O, A, B, C không cùng thuộc một mặt phẳng. Từ điểm D kẻ đường thẳng song song ( hoặc trùng ) với đường thẳng OC, cắt mặt phẳng ( OAB ) tại điểm D ” ( h. 91 ). Khi đó OD-OD + D.D. Theo định lí 1, ta có những số m, n sao cho OD ’ ’ = mā + nb. Ngoài ra do D’D và c cùng phương nên có số p để D’D = pẽ. Vậy Hình 9 / OD = md + nb + pc. Giả sử còn có OD = m a + n } + p °C thì Vì ä, b, c không đồng phẳng nên m – m ’ = n − n ’ = p − p ’ = 0 hay m = m ”, n = n ”, p = p ”. Suy ra những số m, n, p là duy nhất. O 89 Bài toán 3 Cho hình hộp ABCD.A ’ B’C ’ D ’. Xét những điểm M và N lần lượt thuộc những đường thẳng AC và CD sao cho MA ’ = kMC, NC ’ = [ ND ( k và 1 đều khác 1 ). Đặt BA = ä, BB ’ = b, BC = c. a ). Hãy biểu lộ những vectơ BM và BN qua những vectơ ä, b. エ. b ) Xác định những số k, 1 để đường thẳng MN song song với đường thẳng BD ’. Gidi ( h. 92 ) a ) Từ giả thiết ta có : BM = * * : 75 –, do đó1-k BM = – + – B — : 1 – k 1 – k 1 – k BN = foo ” ( # 2, do đó1 – 1 – 1 :. Hình 92 BN = — — — ā + b + cmb ). Vì BD ’ và CD là hai đường thẳng chéo nhau và N thuộc đường thẳng C’D nên đường thẳng MN không hề trùng với đường thẳng BD ’. Vậy đường thẳng MN song song với đường thẳng BD’khi và chỉ khi MN = pBD ”. Do MN = BN – BM nên ta có 两 – 古一古 、 k 片 1 – 1 1 – k 1 一1 1 一从 1 – k Mặt khác BD = d + b + c ( quy tắc hình hộp ) mà ä, b, c là ba vectơ không đồng phẳng nênMN = pBD – – = p c = – 1, k = – 3, p = p1 + — 1 – k Ba vectơ a, b, c có đồng phẳng không nếu một trong hai điều sau đây xảy ra ? a ) Có một vectơ trong ba vectơ đó bằng 0. b ) Có hai vectơ trong ba vectơ đó cùng phương. Cho hình chóp S.ABCD. a ) Chứng minh rằng nếu ABCD là hình bình hành thì SB + SD = SA + SC. Điều ngược lại có đúng không ? b ). Gọi O là giao điểm của AC và BD. Chứng tỏ rằng ABCD là hình bình hành khi và chỉ khi SA + SB + SC + SD = 4SO. Cho hình lăng trụ tam giác ABC.A ’ B’C ’. Gọi G và G ” lần lượt là trọng tâm của tam giác ABC và A’B ’ C ’, I là giao điểm của hai đường thẳng AB ” và A’B. Chứng minh rằng những đường thẳng GI và CG’song song với nhau. Cho hình hộp ABCD A’B ’ C’D ’. Gọi M và N lần lượt là trung điểm của CD và DD ” : G và G ” lần lượt là trọng tâm của những tứ diện A’D ’ MN và BCC’D ’. Chứng minh rằng đường thẳng GG ” và mặt phẳng ( ABB’A ’ ) song song với nhau. Trong không gian cho tam giác ABC. a ) Chứng minh rằng nếu điểm M thuộc mp ( ABC ) thì có ba số x, y, z mà x + y + z = 1 sao cho OM = xOẢ + yOB + zOC với mọi điểm O. b ). Ngược lại, nếu có một điểm O trong không gian sao cho OM = \ OA + yOB + zOC, trong đó x + y + z = 1 thì điểm M thuộc mp ( ABC ). Cho hình chóp S.ABC. Lấy những điểm A, B, C ” lần lượt thuộc những tia SA, SB, SC sao cho SA = aSA ’, SB = bSB ’, SC = CSC, trong đó a, b, c là những số biến hóa. Chứng minh rằng mặt phẳng ( A’B ’ C ’ ) đi qua trọng tâm của tam giác ABC khi và chỉ khi a + b + c = 3.91

Source: https://vh2.com.vn
Category : Trái Đất