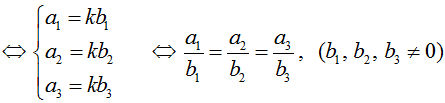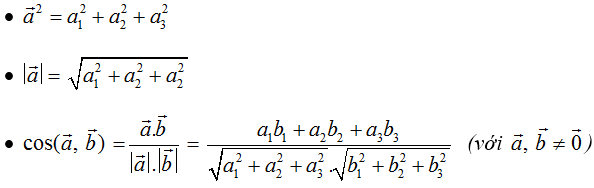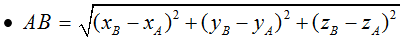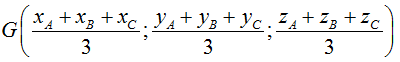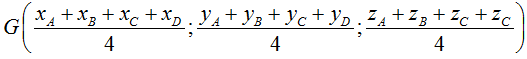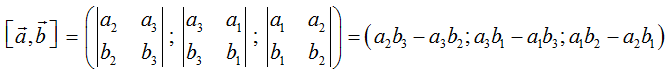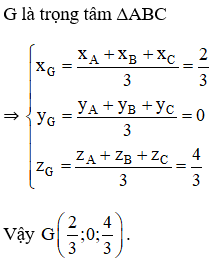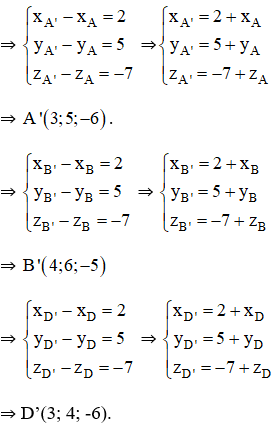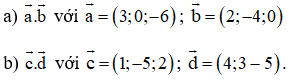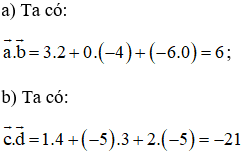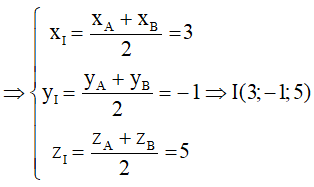Hệ tọa độ trong không gian – Giải bài tập SGK Toán 12

5/5 – ( 8 votes )

Vậy là kiến thức trong chương trình lớp 12 dần đi vào kết thúc rồi, các em đã nắm vững và hiểu được hết các bài chưa? Bài học hôm nay sẽ liên quan đến một chủ đề mà lớp 10 chúng ta đã học. Ở lớp 10, các em được học về tọa độ trong một mặt phẳng, tọa độ Oxy, sang lớp 12, bài học này các em sẽ được học mở rộng và nâng cao hơn: Hệ tọa độ trong không gian. Lượng kiến thức về hệ tọa độ trong không gian khá quan trọng, có mặt trong đề thi THPT Quốc Gia sắp tới, các em hãy học thật tốt và nắm vững kiến thức ngay từ đầu nhé! Giờ thì đến với bài học để chúng ta giải quyết các vấn đề gặp phải nào!

Mục tiêu bài giảng

Bài giảng gồm có những phần kiến thức và kỹ năng sau đây :

• Điểm, đường thẳng, vecto, mặt phẳng trong tọa độ không gian
• Các ví dụ minh họa
• Hướng dẫn giải bài tập SGK
• Bài tập tự luyện

Lý thuyết cần nắm Hệ tọa độ trong không gian

Các em cần nắm vững kiến thức và kỹ năng cơ bản trước khi mở màn làm bài tập !

1.Tọa độ của điểm và của Vecto

Trong không gian, xét ba trục tọa độ Ox, Oy, Oz vuông góc với nhau từng đôi một và chung một điểm gốc O. Gọi i→, j→, k→ là các vectơ đơn vị, tương ứng trên các trục Ox, Oy, Oz. Hệ ba trục như vậy gọi là hệ trục tọa độ vuông góc trong không gian.

Chú ý: 

2. Tọa độ của vectơ

a) Định nghĩa: u→ = (x; y; z) ⇔ k→ = xi→ + yj→ + zk→

b) Tính chất: Cho a→ = (a1; a2; a3), b→ = (b1; b2; b3), k ∈ R

• a→ ± b→ = (a1 ± b1; a2 ± b2; a3 ± b3; )

• ka→ = (ka1; ka2; ka3)

• 0→ = (0; 0; 0), i→ = (1; 0; 0), j→ = (0; 1; 0), k→ = (0; 0; 1)

• a→ cùng phương b→ (b→ ≠ 0→) ⇔ a→ = kb→ (k ∈ R)

• a→.b→ = a1.b1 + a2.b2 + a3.b3

• a→ ⊥ b→ ⇔ a1b1 + a2b2 + a3b3 = 0

3. Tọa độ của điểm

a) Định nghĩa: M(x; y; z) ⇔ OM→ = x.i→ + y.j→ + z.k→ (x : hoành độ, y : tung độ, z : cao độ)

Chú ý: • M ∈ (Oxy) ⇔ z = 0; M ∈ (Oyz) ⇔ x = 0; M ∈ (Oxz) ⇔ y = 0

• M ∈ Ox ⇔ y = z = 0 ; M ∈ Oy ⇔ x = z = 0 ; M ∈ Oz ⇔ x = y = 0 .

b) Tính chất: Cho A(xA; yA; zA), B(xB; yB; zB)

• AB→ = (xB – xA; yB – yA; zB – zA)

• Toạ độ trung điểm của đoạn thẳng AB :

• Toạ độ trọng tâm G của tam giác ABC :

• Toạ độ trọng tâm G của tứ diện ABCD :

4. Tích có hướng của hai vectơ

a) Định nghĩa: Trong không gian Oxyz cho hai vectơ a→ = (a1; a2; a3), b→ = (b1; b2; b3). Tích có hướng của hai vectơ a→ và b→ kí hiệu là [a→, b→], được xác định bởi

Chú ý: Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số.

b) Tính chất:

• [a→, b→] ⊥ a→; [a→, b→] ⊥ b→

• [a→, b→] = -[b→, a→]

• [i→, j→] = k→; [j→, k→] = i→; [k→, i→] = j→

• |[a→, b→]| = |a→|.|b→|.sin(a→, b→) (Chương trình nâng cao)

• a→, b→ cùng phương ⇔ [a→, b→] = 0→ (chứng minh 3 điểm thẳng hàng)

c) Ứng dụng của tích có hướng: (Chương trình nâng cao)

• Điều kiện đồng phẳng của ba vectơ: a→, b→ và c→ đồng phẳng ⇔ [a→, b→].c→ = 0

• Diện tích hình bình hành ABCD: SABCD = |[AB→], AD→|

• Diện tích tam giác ABC: SABC = 1/2 |[AB→], AC→|

• Thể tích khối hộp ABCDA’B’C’D’ : VABCD.A’B’C’D’ = |[AB→, AD→].AA’→|

• Thể tích tứ diện ABCD: VABCD = 1/6 |[AB→, AC→].AD→|

Giải bài tập SGK Hệ tọa độ không gian

Tổng hợp bài tập và giải thuật SGK do iToan biên soạn cụ thể và đúng mực, gúp em học tập thuận tiện hơn !

Bài 1

Cho ba vectơ : a → = ( 2 ; – 5 ; 3 ), b → = ( 0 ; 2 ; – 1 ), c → = ( 1 ; 7 ; 2 )
a ) Tính tọa độ của vectơ d → = 4 a → – 1/3 b → + 3 c →
b ) Tính tọa độ của vectơ e → = a → – 4 b → – 2 c →

Lời giải:

a ) Ta có : 4 a → = ( 8 ; – 20 ; 12 )
– 1/3 b → = ( 0 ; – 2/3 ; 1/3 )
3 c → = ( 3 ; 21 ; 6 )
Vậy d → = 4 a → – 1/3 b → + 3 c → = ( 11 ; 1/3 ; 55/3 )
b ) Ta có : – 4 b → = ( 0 ; – 8 ; 4 )
– 2 c → = ( – 2 ; – 14 ; – 4 )
Vậy e → = a → – 4 b → – 2 c → = ( 0 ; – 27 ; 3 )

Bài 2 

Cho ba điểm A ( 1 ; – 1 ; 1 ), B ( 0 ; 1 ; 2 ), C ( 1 ; 0 ; 1 ). Tìm tọa độ trọng tâm G của tam giác ABC .

Lời giải:

Bài 3

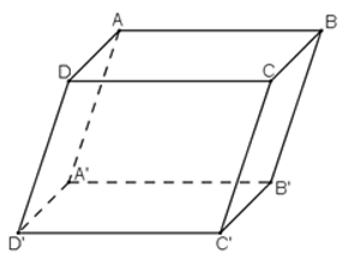
Cho hình hộp ABCD.A ’ B’C ’ D ’ biết A ( 1 ; 0 ; 1 ), B ( 2 ; 1 ; 2 ), D ( 1 ; – 1 ; 1 ), C ‘ ( 4 ; 5 ; – 5 ). Tính tọa độ những đỉnh còn lại của hình hộp .

Lời giải:

Bài 4: Tính:

Lời giải:

Bài 5

Tìm tâm và nửa đường kính của những mặt cầu sau đây :
a ) x2 + y2 + z2 – 8 x – 2 y + 1 = 0
b ) 3×2 + 3 y2 + 3 z2 – 6 x + 8 y + 15 z – 3 = 0

Lời giải:

Bài 6 

Lập phương trình mặt cầu trong hai trường hợp sau đây :
a ) Có đường kính AB với A ( 4 ; – 3 ; 7 ), B ( 2 ; 1 ; 3 )
b ) Đi qua điểm A ( 5 ; – 2 ; 1 ) và có tâm C ( 3 ; – 3 ; 1 )

Lời giải:

Lời kết

Sau bài học này, các em đã hiểu về hệ tọa độ trong không gian chưa? Kiến thức về hệ tọa độ trong không gian có nhiều công thức, đòi hỏi khả năng ghi nhớ và tư duy, vận dụng cao, vì vậy hãy chăm chỉ làm thật nhiều bài tập để luyện tập và ghi nhớ bài học nhé! Các em siêng năng làm bài và tìm tòi nhiều dạng bài tập sẽ càng được nâng cao và củng cố kiến thức hơn. Để ôn tập về bài giảng này cũng như các bài giảng khác trong chương trình lớp 12, các em có thể truy cập vào web Toppy.

Toppy là công ty Edtech về giáo dục trực tuyến, phân phối thưởng thức học tập cá thể cho hàng trăm nghìn học viên, sinh viên và nhà trường để giải đáp những nhu yếu trong việc học tập trải qua mạng lưới những chuyên viên và giáo viên khắp toàn thế giới mà Toppy gọi là những gia sư học thuật quốc tế. Với kho tàng kỹ năng và kiến thức khổng lồ theo từng chủ đề, bám sát chương trình sách giáo khoa, những thầy cô Toppy luôn nỗ lực mang đến cho những em những bài giảng hay, dễ hiểu nhất, giúp những em văn minh hơn từng ngày .

Chúc các bạn sẽ thành công trong việc làm chủ môn Giải tích 11 và đạt thật nhiều điểm thưởng. 

Source: https://vh2.com.vn
Category : Trái Đất