Khắc phục nhanh chóng lỗi E-01 trên tủ lạnh Bosch https://appongtho.vn/tu-lanh-bosch-bao-loi-e01-cach-kiem-tra Tại sao mã lỗi E-01 xuất hiện trên tủ lạnh Bosch? Nguyên nhân và quy trình sửa lỗi E-01...
Điện trường – Wikipedia tiếng Việt
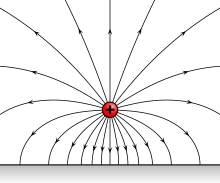 Điện trường phát ra từ một điện tích điểm dương
Điện trường phát ra từ một điện tích điểm dương
Điện trường là một trường điện tạo ra từ các đường lực điện bao quanh lấy điện tích. Điện trường có thể được biểu diễn bằng các đường sức điện. Vector cường độ điện trường tại bất kì điểm nào trên đường sức điện có phương trùng với tiếp tuyến tại điểm đó trên đường sức điện và có chiều trùng với chiều của đường sức. Tập hợp các đường sức cường độ điện trường gọi là điện phổ.
Điện trường rất quan trọng trong nhiều nghành nghề dịch vụ vật lý và được khai thác thực tiễn trong công nghệ tiên tiến điện. Ở quy mô nguyên tử, điện trường là lực tương tác chính giữa hạt nhân và những electron trong nguyên tử. Điện trường và từ trường đều là bộc lộ của lực điện từ, một trong bốn lực cơ bản ( hoặc tương tác cơ bản ) của tự nhiên .
Cường độ điện trường[sửa|sửa mã nguồn]
Cường độ điện trường[sửa|sửa mã nguồn]
Cường độ điện trường là đại lượng đặc trưng cho điện trường về phương diện tác dụng lực. Một điện tích, q, nằm trong điện trường có cường độ điện trường, thể hiện bằng vectơ
E
→
{\displaystyle {\vec {E}}}

F
→
{\displaystyle {\vec {F}}}

-
-
F
→=
q
.E
→{\displaystyle {\vec {F}}=q.{\vec {E}}}
Bạn đang đọc: Điện trường – Wikipedia tiếng Việt
-
Vậy ,
-
- E → = F → / q { \ displaystyle { \ vec { E } } = { \ vec { F } } / q }
- E → = F → / q { \ displaystyle { \ vec { E } } = { \ vec { F } } / q }
Cường độ điện trường gây ra bởi điện tích điểm được tính bằng công thức :
- E = q 4 π ε 0 ε r 2 { \ displaystyle E = { \ frac { q } { 4 \ pi \ \ varepsilon _ { 0 } \ varepsilon \ r ^ { 2 } } } }
trong đó
- q là độ lớn điện tích
- ε 0 { \ displaystyle \ varepsilon _ { 0 } }
độ điện thẩm chân không
- ε { \ displaystyle \ varepsilon \ }
hằng số điện môi của môi trường
- r là khoảng cách từ điện tích đến điểm ta xét
Với cường độ điện trường này, một điện tích khác nằm trong nó sẽ chịu lực điện tỷ suất thuận với tích hai điện tích và tỷ suất nghịch với bình phương khoảng cách. Đó chính là lực Coulomb .Để tính được điện trường do một vật mang điện ( điện tích ) gây ra, hoàn toàn có thể chia nó ra thành nhiều vật nhỏ hơn. Nếu phép chia tiến đến một số lượng giới hạn nào đó, vật nhỏ mang điện sẽ trở thành một điện tích. Khi đó hoàn toàn có thể vận dụng nguyên tắc chồng chất cho điện trường ( hay còn gọi là nguyên tắc tính năng độc lập ) .
Cường độ điện trường tại một điểm trong điện trường do N điện tích điểm gây ra bằng tổng vectơ cường độ điện trường do từng điện tích điểm gây ra tại điểm đó.
Cường độ điện trường của vật dẫn điện[sửa|sửa mã nguồn]
Điện tích điểm hình cầu[sửa|sửa mã nguồn]
- D = Q A = ϵ E { \ displaystyle D = { \ frac { Q } { A } } = \ epsilon E }
Cường độ điện trường của một hình cầu tròn có diện tích
A
=
4
π
r
2
{\displaystyle A=4\pi r^{2}}

- E = Q ϵ A = Q ϵ 4 π r 2 { \ displaystyle E = { \ frac { Q } { \ epsilon A } } = { \ frac { Q } { \ epsilon 4 \ pi r ^ { 2 } } } }
Cường độ điện lượng
- Q. = D A = ( ϵ E ) A { \ displaystyle Q = DA = ( \ epsilon E ) A }
Điện tích khác loại có cùng điện lượng[sửa|sửa mã nguồn]
Lực Coulomb của 2 điện tích khác loại có cùng điện lượng
-
F
=
kQ
2
r
2
{\displaystyle F=k{\frac {Q^{2}}{r^{2}}}}
Q. + = Q − { \ displaystyle Q_ { + } = Q_ { – } }
Lực này tương tác với điện tích tạo ra điện trường
- E = F Q = k Q 2 r 2 Q = k Q. r 2 { \ displaystyle E = { \ frac { F } { Q } } = { \ frac { k { \ frac { Q ^ { 2 } } { r ^ { 2 } } } } { Q } } = k { \ frac { Q } { r ^ { 2 } } } }
Tụ điện tạo ra từ 2 mặt phẳng song song có cường độ điện trường
- E = V l { \ displaystyle E = { \ frac { V } { l } } }
Định luật Gauss về Điện trường[sửa|sửa mã nguồn]
- Φ = ∮ S E ⋅ d A = 1 ϵ o ∫ V ρ d V = Q A ϵ o { \ displaystyle \ Phi = \ oint _ { S } \ mathbf { E } \ cdot d \ mathbf { A } = { 1 \ over \ epsilon _ { o } } \ int _ { V } \ rho \ dV = { \ frac { Q_ { A } } { \ epsilon _ { o } } } }
Với
- Φ { \ displaystyle \ Phi }
thông lượng điện,
- E { \ displaystyle \ mathbf { E } }
- d A { \ displaystyle d \ mathbf { A } }
S,
- Q. A { \ displaystyle Q_ { \ mathrm { A } } }
- ρ { \ displaystyle \ rho }
- V { \ displaystyle V }
ϵ o { \ displaystyle \ epsilon _ { o } }
hằng số điện của không gian tự do và ∮ S { \ displaystyle \ oint _ { S } }
S bao phủ thể tích V.
- ∇ ⋅ E = ρ ϵ 0 { \ displaystyle \ nabla \ cdot \ mathbf { E } = { \ frac { \ rho } { \ epsilon _ { 0 } } } }
Với
Xem thêm: Thư tình: Hãy cho anh cơ hội bên em
- ∇ { \ displaystyle \ nabla }
toán tử div,
- E { \ displaystyle \ mathbf { E } }
- ρ là mật độ điện tích (đơn vị C/m³),
Liên kết ngoài[sửa|
sửa mã nguồn]
Source: https://vh2.com.vn
Category : Cơ Hội




















