Trước đây, chúng ta đã nghiên cứu các tính chất của những hình nằm trong mặt phẳng. Môn học nghiên cứu các tính chất của hình nằm trong mặt phẳng được gọi là Hình học phẳng. Trong thực tế, ta thường gặp các vật như: hộp phấn, kệ sách, bàn học… là các hình trong không gian. Môn học nghiên cức các tính chất của các hình trong không gian được gọi là Hình học không gian.

LÝ THUYẾT

Khái niệm khởi đầu

1. Mặt phẳng

Mặt phẳng là một đối tượng người dùng của toán học. Mặt phẳng không có bề dày và không có số lượng giới hạn .

• Để biểu diễn tả mặt phẳng ta thường dùng hình bình hành hay một miền góc và ghi tên của mặt phẳng vào một góc của hình biểu diễn.

• Để kí hiệu mặt phẳng, ta thường dùng các chữ cái in hoa hoặc chữ cái Hi Lạp đặt trong dấu ngoặc “( )”.

Ví dụ: mặt phẳng (P) hoặc viết tắt mp(P)…

2. Điểm thuộc mặt phẳng

Cho điểm A và mặt phẳng ( a )

• Điểm A thuộc mặt phẳng (a) ta nói A nằm trên (a) hay (a) chứa A hoặc (a) đi qua A. Kí hiệu: A (a).

• Điểm A không thuộc mặt phẳng (a) ta nói A nằm ngoài (a) hay (a) không chứa A hoặc (a) không đi qua A. Kí hiệu: A (a).

3. Hình biểu diễn của một hình không gian

Để nghiên cứu hình học không gian người ta thường vẽ các hình không gian lên bảng, lên giấy. Ta gọi hình vẽ đó là hình biểu diễn của một hình không gian. Hình biểu diễn được vẽ dựa vào các quy tắc:

• Hình biểu diễn của đường thẳng là đường thẳng, của đoạn là đoạn thẳng
• Hình biểu diễn của hai đường thẳng song song là hai đường thẳng song song, của hai đường thẳng cắt nhau là hai đường thẳng cắt nhau
• Hình biểu diễn phải giữ nguyên quan hệ thuộc giữa các điểm và đường thẳng
• Dùng nét liền để biển diễn những đường nhìn thấy, nét đứt đoạn biểu diễn những đường bị che khuất

Các đặc thù / tiên đề thừa nhận

Để nghiên cứu và điều tra hình học khoảng trống, từ quan sát thực tiễn và kinh nghiệm tay nghề, người ta thừa nhận một số ít đặc thù / tiên đề sau :

• Tiên đề 1. Có duy nhất một đường thẳng đi qua hai điểm phân biệt.

• Tiên đề 2. Có duy nhất một mặt phẳng đi qua 3 điểm không thẳng hàng.

Mặt phẳng đi qua 3 điểm 𝐴, 𝐵, 𝐶 kí hiệu là ( 𝐴𝐵𝐶 ) .

• Tiên đề 3. Nếu trên đường thẳng 𝑑d có 2 điểm phân biệt 𝐴 và 𝐵 thuộc mặt phẳng (𝛼) thì mọi điểm trên 𝑑d đều thuộc (𝛼).

Khi đó ta nói đường thẳng 𝑑d nằm trong mặt phẳng ( 𝛼 ) ( α ) và ghi 𝑑 ⊂ ( 𝛼 ), hoặc nói ( 𝛼 ) chứa 𝑑 và ghi ( 𝛼 ) ⊃ 𝑑 .

• Tiên đề 4. Tồn tại 4 điểm không cùng thuộc một mặt phẳng.

Nếu có nhiều điểm cùng thuộc một mặt phẳng thì ta nói những điểm đó đồng phẳng, còn nếu không có mặt phẳng nào chứa các điểm đó thì ta nói rằng chúng không đồng phẳng.

• Tiên đề 5. Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng còn có một điểm chung khác nữa.

Áp dụng tiên đề 3 thì hai mặt phẳng này có vô số điểm chung nằm trên một đường thẳng, đường thẳng này gọi là giao tuyến của hai mặt phẳng và ghi (𝛼)∩(𝛽)=𝑑.

• Tiên đề 6. Trên mỗi mặt phẳng, các kết quả đã biết trong hình học phẳng đều đúng.

Nghĩa là xét riêng trong một mặt phẳng nào đó, ta được phép sử dụng những kỹ năng và kiến thức hình học phẳng đã học ở lớp dưới .

Cách xác lập một mặt phẳng

Ba cách xác định mặt phẳng:

a) Mặt phẳng được hoàn toàn xác định khi biết nó đi qua ba điểm không thẳng hàng.

Mặt phẳng qua ba điểm không thẳng hàng A, B, C kí hiệu là : mp ( ABC ) hoặc ( ABC )

b) Mặt phẳng được hoàn toàn xác định khi biết nó đi qua một điểm và chứa một đường thẳng không đi qua điểm đó.

Cho đường thẳng d và điểm A không nằm trên d, khi đó ta xác lập được mặt phẳng, kí hiệu là : mp ( A, d ) hay ( A, d )

c) Mặt phẳng được hoàn toàn xác định khi biết nó chứa hai đường thẳng cắt nhau.

Cho hai đường thẳng cắt nhau a và b. Khi đó hai đường thẳng a và b xác lập một mặt phẳng và kí hiệu là : mp ( a, b ) hay ( a, b ), hoặc mp ( b, a ) hay ( b, a ) .

BIỂU DIỄN MỘT SỐ HÌNH TRONG KHÔNG GIAN

• Hình tứ diện
• Hình chóp
• Hinhg lăng trụ
• Hình hộp

Tên hình, cách biểu diễn	Hình biểu diễn	Các khái niệm và tính chất
Tứ diện ABCD
Tứ diện đều ABCD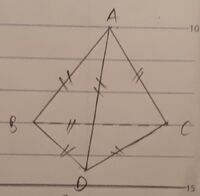
Hình chóp S.ABC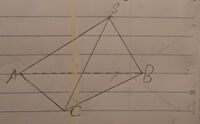
Hình chóp đều S.ABC
Hình chóp S.ABCD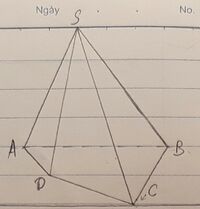
Hình chóp đều S.ABCD
Hình lăng trụ ABC.A’B’C’
Hình lăng trụ đứng ABC.A’B’C’
Hình lăng trụ đều ABC.A’B’C’
Hình lăng trụ ABCD.A’B’C’D’
Hình hộp ABCD.A’B’C’D’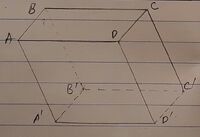

DẠNG BÀI TẬP

4 cách xác định mặt phẳng trong không gian

• Qua 3 điểm A,B,C không thẳng hàng, có 1 và chỉ 1 mặt phẳng. Kí hiệu: (ABC)
• Qua 1 điểm A và một đường thẳng a không qua A có 1 và chỉ 1 mặt phẳng. Kí hiệu: (A,a)
• Qua 2 đường thẳng cắt nhau a và b có 1 và chỉ 1 mặt phẳng. Kí hiệu: (a,b)
• Qua 2 đường thẳng a và b song song có 1 và chỉ 1 mặt phẳng. Kí hiệu: (a,b)

Dạng 1 : Tìm giao tuyến của 2 mặt phẳng

• Tìm 2 điểm chung rồi nối lại
• Tìm điểm chung thứ nhất thường nhìn thấy trong tên gọi hoặc trong hình vẽ
• Điểm chung thứ hai thường là giao điểm của 2 đường thẳng lần lượt nằm trong 2 mặt phẳng, nhưng cắt nhau trong mặt phẳng thứ ba

Dạng 2 : Tìm giao điểm của đường thẳng và mặt phẳng

Muốn tìm M ≡ a ∩ ( α )

Cách 1

• a ∩ b ≡ M
• b ⊂ (α)

⇒ M ≡ a ∩ ( α )

Cách 2

• Chọn a ⊂ (β)
• Tìm (β) ∩ (α) = Δ

⇒ Δ ∩ a ≡ M cần tìm

Dạng 3 : Chứng minh 3 điểm thẳng hàng

Để chứng minh 3 điểm A,B,C thẳng hàng, ta chỉ ra đó là 3 điểm chung của 2 mặt phẳng phân biệt.

Dạng 4 : Chứng minh 3 đường thẳng đồng quy

Để chứng tỏ 3 đường thẳng a, b, c đômgf quy, ta gọi I là giao của a và b. Lấy 2 điểm M, N ∈ c và chứng tỏ 3 điểm I, M, N thẳng hàng .

Dạng 5 : Tìm thiết diện

Muốn tìm thiết diện của ( P ) với hình chóp, ta dùng 1 trong 2 cách :

• Cách 1: Tìm giao tuyến của (P) với từng mặt của hình chóp
• Cách 2: Tìm giao điểm của (P) với từng mặt của hình chóp

Giao điểm ở phần kéo dài của cạnh không được tính là một đỉnh của thiết diện.

Source: https://vh2.com.vn
Category : Khoa Học