Đại cương dòng điện xoay chiều ( đầy đủ)

Lý thuyết về suất điện động xoay chiều, những bài toán về thời gian, điện lượng và giá trị thức thời, hiệu dụng và cực đại là những kiến thức được trình bày rất chi tiết trong bài viết này. Bên cạnh đó những bài tập có lời giải chi tiết giúp bạn đọc củng cố kiến thức hơn.

ĐẠI CƯƠNG DÒNG ĐIỆN XOAY CHIỀU

A. Tóm tắt lí thuyết :

I.Cách tạo ra suất điện động xoay chiều:

Cho khung dây dẫn phẳng có N vòng, diện tích quy hoạnh Squay đều với tốc độ ω, xung quanh trục vuông góc với với những đườngsức từ của một từ trường đều có cảm ứng từ \ ( \ vec { B } \ ). Theo định luật cảmứng điện từ, trong khung dây Open một suất điện động đổi kháctheo định luật dạng cosin với thời hạn gọi tắt là suất điện động xoay chiều : \ ( e = E_ { o } cos ( \ omega t + \ varphi _ { 0 } ) \ )

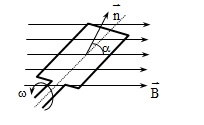
2.Từ thông gởi qua khung dây :

– Từ thông gửi qua khung dây dẫn gồm N vòng dây có diện tích quy hoạnh S quay trong từ trường đều \ ( \ vec { B } \ ). Giả sử tại t = 0 thì : \ ( ( \ vec { n }, \ vec { B } ) = \ varphi \ )- Biểu thức từ thông của khung : \ ( \ Phi = NBScos \ omega t = \ Phi _ { 0 }. cos \ omega t \ )- Từ trải qua khung dây cực lớn \ ( \ Phi _ { 0 } = NBS \ ) ; ω là tần số góc bằng vận tốc quay của khung ( rad / s )Đơn vị : + Φ : Vêbe ( Wb ) ;+ S : Là diện tích quy hoạnh một vòng dây ( S : mét vuông ) ;+ N : Số vòng dây của khung+ \ ( \ vec { B } \ ) : Véc tơ cảm ứng từ của từ trường đều. B : Tesla ( T ) ( \ ( \ vec { B } \ ) vuông góc với trục quay ∆ )+ ω : Vận tốc góc không đổi của khung dây( Chọn gốc thời hạn t = 0 lúc ( \ ( ( \ vec { n }, \ vec { B } ) = 0 ^ { 0 } \ ) )- Chu kì và tần số của khung : \ ( T = \ frac { 2 \ pi } { \ omega } ; f = \ frac { 1 } { T } \ )

3. Suất điện động xoay chiều:

– Biểu thức của suất điện động cảm ứng tức thời :

\(e=\frac{-\Delta \Phi }{\Delta t}=-\Phi ‘=\omega NBS.sin\omega\)\(t=E_{o}cos(\omega t-\frac{\pi }{2})\)  

\ ( e = E_ { o } cos ( \ omega t + \ varphi _ { 0 } ) \ ) Đặt \ ( E_ { 0 } = NB \ omega S \ ) : Suất điện động cực lớn\ ( \ varphi _ { 0 } = \ varphi – \ frac { \ pi } { 2 } \ )Đơn vị : e, E0 ( V )

II.Điện áp xoay chiều -Dòng điện xoay chiều.

1.Biểu thức điện áp tức thời:

Nếu nối hai đầu khung dây với mạch ngoài thành mạch kín thì biểu thức điện áp tức thời mạch ngoài là : u = e-irXem khung dây có r = 0 thì u = \ ( e = E_ { o } cos ( \ omega t + \ varphi _ { 0 } ) \ ) .

Tổng quát : \(u=U_{o}cos(\omega t+ \varphi _{u})\) ( \(\varphi _{u}\) là pha ban đầu của  điện áp )

2.Khái niệm về dòng điện xoay chiều

– Là dòng điện có cường độ biến thiên tuần hoàn với thời hạn theo quy luật của hàm số sin hay cosin, với dạng tổng quát : \ ( i = I_ { o } cos ( \ omega t + \ varphi _ { i } ) \ )* i : giá trị của cường độ dòng điện tại thời gian t, được gọi là giá trị tức thời của i ( cường độ tức thời ) .* I0 > 0 : giá trị cực lớn của i ( cường độ cực lớn ). * ω > 0 : tần số góc .f : tần số của i. T : chu kì của i. * ( ωt + φ ) : pha của i. * φi là pha khởi đầu của dòng điện )

3.Độ lệch pha giữa điện áp u và cường độ dòng điện i:
Đại lượng : φ = φu -φi gọi là độ lệch pha của u so với i.

Nếu φ > 0 thì u sớm pha ( nhanh pha ) so với i .Nếu φNếu φ = 0 thì u đồng pha ( cùng pha ) so với i .

4. Giá trị hiệu dụng  :Dòng điện xoay chiều cũng có tác dụng toả nhiệt như dòng điện một chiều.Xét về mặt toả nhiệt trong một thời gian dài thì dòng điện xoay chiều \(i=I_{o}cos(\omega t+ \varphi _{i})\)  tương đương với dòng điện một chiều có cường độ không đổi có cường độ bằng \(\frac{I_{0}}{\sqrt{2}}\).

” Cường độ hiệu dụng của dòng điện xoay chiều bằng cường độ của một dòng điện không đổi, nếu cho hai dòng điện đó lần lượt đi qua cùng một điện trở trong những khoảng chừng thời hạn bằng nhau đủ dài thì nhiệt lượng toả ra bằng nhau. Nó có giá trị bằng cường độ dòng điện cực lớn chia cho \ ( \ sqrt { 2 } \ ) ” .Các giá trị hiệu dụng của dòng điện xoay chiều :- Giá trị hiệu dụng : + Cường độ dòng điện hiệu dụng : I = \ ( \ frac { I_ { 0 } } { \ sqrt { 2 } } \ )+ Hiệu điện thế hiệu dụng : U = \ ( \ frac { U_ { 0 } } { \ sqrt { 2 } } \ )+ Suất điện động hiệu dụng : E = \ ( \ frac { E_ { 0 } } { \ sqrt { 2 } } \ )

*Lý do sử dụng các giá trị hiệu dụng của dòng điện xoay chiều:

— Khi sử dụng dòng điện xoay chiều, ta không cần chăm sóc đến những giá trị tức thời của i và u vì chúngbiến thiên rất nhanh, ta cần chăm sóc tới công dụng của nó trong một thời hạn dài .- Tác dụng nhiệt của dòng điện tỉ lệ với bình phương cường độ dòng điện nên không nhờ vào vàochiều dòng điện .- Ampe kế đo cường độ dòng điện xoay chiều và vôn kế đo điện áp xoay chiều dựa vào công dụng nhiệt của dòng điện nên gọi là ampe kế nhiệt và vôn kế nhiệt, số chỉ của chúng là cường độ hiệu dụng và điện áp hiệu dụng của dòng điện xoay chiều .

5.  Nhiệt lượng toả ra trên điện trở R trong thời gian t nếu có dòng điện xoay chiều i(t) = I0cos(ωt + φi) chạy qua là: Q = RI2t

 6.Công suất toả nhiệt trên R khi có ddxc chạy qua :  P=RI2

B. CÁC DẠNG BÀI TẬP:

Dạng 1: XÁC ĐỊNH SUẤT ĐIỆN ĐỘNG CẢM ỨNG

1.Phương pháp:

Thông thường bài tập thuộc dạng này yêu cầu ta tính từ thông, suất điện động cảm ứng xuất hiện trong

khung dây quay trong từ trường. Ta sử dụng các công thức sau để giải:

– Tần số góc:  \(\omega =2\pi n_{0}\), Với n0 là số vòng quay trong mỗi giây bằng tần số dòng điện xoay chiều.

– Biểu thức từ thông: \(\Phi =\Phi _{0}cos(\omega t+\varphi )\) ,  Với  \(\Phi _{0}\)  = NBS.

– Biểu thức suất điện động: \(e=E_{0}cos(\omega t+\varphi )\)  Với Eo = NBSω ; \(\varphi =(\vec{n},\vec{B})\)  lúc t=0.

– Vẽ đồ thị: Đồ thị là đường hình sin:   * có chu kì :  \(T=\frac{2\pi }{\omega }\)        * có biên độ: E0

2.Bài tập áp dụng :

Bài  1 : Một khung dây dẫn phẳng có diện tích S = 50 cm2, có N = 100 vòng dây, quay đều với tốc độ 50 vòng/giây quanh một trục vuông góc với các đường sức của một từ trường đều có cảm ứng từ B = 0,1 T. Chọn gốc thời gian t = 0 là lúc vectơ pháp tuyến \(\vec{n}\) của diện tích S của khung dây cùng chiều với vectơ cảm ứng từ  \(\overrightarrow{B}\) và chiều dương là chiều quay của khung dây.

a ) Viết biểu thức xác lập từ thông Φ qua khung dây .b ) Viết biểu thức xác lập suất điện động e Open trong khung dây .c ) Vẽ đồ thị màn biểu diễn sự biến hóa của e theo thời hạn .

Bài  giải :

a ) Khung dây dẫn quay đều với vận tốc góc : ω = 50.2 π = 100 π rad / s

Tại thời gian bắt đầu t = 0, vectơ pháp tuyến \ ( \ vec { n } \ ) của diện tích quy hoạnh S của khung dây có chiều trùng với chiều của vectơ cảm ứng từ \ ( \ overrightarrow { B } \ ) của từ trường. Đến thời gian t, pháp tuyến \ ( \ vec { n } \ ) của khung dây đã quay được một góc bằng ωt. Lúc này từ trải qua khung dây là :\ ( \ Phi = NBS \ ) cos ( ωt )Như vậy, từ trải qua khung dây biến thiên điều hoà theo thời hạn với tần số góc ω và với giá trị cực lớn ( biên độ ) là Ф0 = NBS .Thay N = 100, B = 0,1 T, S = 50 cm2 = 50. 10-4 mét vuông và ω = 100 π rad / s ta được biểu thức của từ trải qua khung dây là : \ ( \ Phi = 0,05 cos ( 100 \ pi t ) \ ) ( Wb )b ) Từ trải qua khung dây biến thiên điều hoà theo thời hạn, theo định luật cảm ứng điện từ của Faraday thì trong khung dây Open một suất điện động cảm ứng .Suất điện động cảm ứng Open trong khung dây được xác lập theo định luật Lentz :\ ( e = – \ frac { d \ Phi } { dt } = – \ Phi ‘ _ { t } = \ omega NBSsin ( \ omega t ) = \ omega NBScos ( \ omega t – \ frac { \ pi } { 2 } ) \ )Như vậy, suất điện động cảm ứng Open trong khung dây đổi khác điều hoà theo thời hạn với tần số góc ω và với giá trị cực lớn ( biên độ ) là E0 = ωNBS .

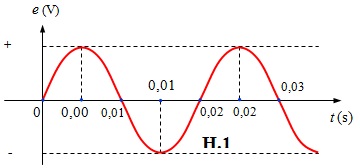
Thay N = 100, B = 0,1 T, S = 50 cm2 = 50. 10-4 mét vuông và ω = 100 π rad / s ta được biểu thức xác lập suất điện động Open trong khung dây là :\ ( e = 5 \ pi cos ( 100 \ pi t – \ frac { \ pi } { 2 } ) \ ) ( V ) hay \ ( e \ approx 15,7 cos ( 314 t – \ frac { \ pi } { 2 } ) \ ) ( V )c ) Suất điện động Open trong khung dây biến hóa điều hoà theo thời hạn với chu khì T và tần số f lần lượt là :\ ( T = \ frac { 2 \ pi } { \ omega } = \ frac { 2 \ pi } { 100 \ pi } = 0,02 s ; f = \ frac { 1 } { T } = \ frac { 1 } { 0,02 } = 50H z \ )Đồ thị màn biểu diễn sự đổi khác của suất điện động e theo thời hạn t là đường hình sin có chu kì tuần hoàn T = 0,02 s. Bảng giá trị của suất điện động e tại một số ít thời gian đặc biệt quan trọng như : 0 s, \ ( \ frac { T } { 4 } = 0,005 s ; \ frac { T } { 2 } = 0,01 s, \ frac { 3T } { 4 } = 0,015 s, T = 0,02 s, \ frac { 5T } { 4 } = 0,025 s \ ) và \ ( \ frac { 3T } { 2 } = 0,03 s \ ) :

Đồ thị biểu diễn sự phụ thuộc của e theo t như hình trên H1  :

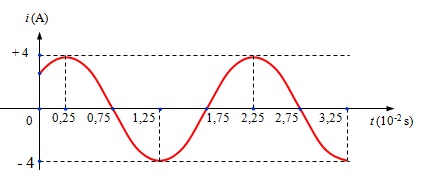
Bài  2 : Dòng điện xoay chiều chạy qua một đoạn mạch có cường độ biến đổi điều hoà theo thời gian được mô tả bằng đồ thị ở hình dưới đây.

a ) Xác định biên độ, chu kì và tần số của dòng điện .b ) Đồ thị cắt trục tung ( trục Oi ) tại điểm có toạ độ bao nhiêu ?

Bài  giải :

a ) Biên độ chính là giá trị cực lớn I0 của cường độ dòng điện. Dựa vào đồ thị ta có biên độ của dòng điện này là : I0 = 4 A .Tại thời gian 2,5. 10-2 s, dòng điện có cường độ tức thời bằng 4 A. Thời điểm sau đó mà dòng điện có cường độ tức thời bằng 4 A là 2,25. 10-2 s. Do đó chu kì của dòng điện này là :T = 2,25. 10-2 – 0,25. 10-2 = 2.10 – 2 s ; Tần số của dòng điện này là : \ ( f = \ frac { 1 } { T } = \ frac { 1 } { 2.10 ^ { – 2 } } = 50H z \ )b ) Biểu thức cường độ dòng điện xoay chiều này có dạng : \ ( i = I_ { 0 } cos ( \ omega t + \ varphi _ { i } ) \ )Tần số góc của dòng điện này là : \ ( \ omega = 2 \ pi f = 2 \ pi. 50 = 100 \ pi ( rad / s ) \ )Tại thời gian t = 0,25. 10-2 s, dòng điện có cường độ tức thời i = I0 = 4 A, nên suy ra :\ ( I_ { 0 } cos ( 100 \ pi. 0 + \ varphi _ { i } ) = I_ { 0 } \ ) Hay \ ( cos ( \ frac { \ pi } { 4 } + \ varphi _ { i } ) = 1 \ )Suy ra : ( \ ( \ varphi _ { i } ) = – \ frac { \ pi } { 4 } rad \ ). Do đó biểu thức cường độ của dòng điện này là :

\ ( i = I_ { 0 } cos ( 100 \ pi t – \ frac { \ pi } { 4 } ) ( A ) = 4 cos ( 100 \ pi t – \ frac { \ pi } { 4 } ) ( A ) \ )Tại thời gian t = 0 thì dòng điện có cường độ tức thời là :\ ( i = I_ { 0 } cos ( 100 \ pi. 0 – \ frac { \ pi } { 4 } ) ( A ) = \ frac { I_ { 0 } } { \ sqrt { 2 } } = \ frac { 4 } { \ sqrt { 2 } } = 2 \ sqrt { 2 } A \ ) \ ( \ approx 2,83 A \ ) .Vậy đồ thị cắt trục tung tại điểm có toạ độ ( 0 s, \ ( 2 \ sqrt { 2 } \ ) A ) .

3.TRẮC NGHIỆM VẬN DỤNG ĐẠI CƯƠNG DDXC

Câu 1. Phát biểu nào sau đây là không đúng?

A. Điện áp đổi khác điều hoà theo thời hạn gọi là điện áp xoay chiều .B. Dòng điện có cường độ đổi khác điều hoà theo thời hạn gọi là dòng điện xoay chiều .C. Suất điện động đổi khác điều hoà theo thời hạn gọi là suất điện động xoay chiều .D. Cho dòng điện một chiều và dòng điện xoay chiều lần lượt đi qua cùng một điện trở thì chúng toả ra nhiệt lượng như nhau .

Câu 2: Nguyên tắc tạo ra dòng điện xoay chiều dựa trên

A. từ trường quay. B. hiện tượng kỳ lạ quang điện .C. hiện tượng kỳ lạ tự cảm. D. hiện tượng kỳ lạ cảm ứng điện từ .

4.TRẮC NGHIỆM  ÔN TẬP

Câu 1. Số đo của vôn kế xoay chiều chỉ

A. giá trị tức thời của điện áp xoay chiều. B. giá trị trung bình của điện áp xoay chiềuC. giá trị cực lớn của điện áp xoay chiều. D. giá trị hiệu dụng của điện áp xoay chiều .

Câu 2. Số đo của Ampe kế xoay chiều chỉ

A. giá trị tức thời của dòng điện xoay chiều .B. giá trị trung bình của dòng điện xoay chiềuC. giá trị cực lớn của dòng điện xoay chiều .D. giá trị hiệu dụng của dòng điện xoay chiều .

DẠNG 2. GIẢI TOÁN  ĐIỆN XOAY CHIỀU BẰNG MỐI LIÊN QUAN GIỮA DDDH VÀ CHUYỂN ĐỘNG TRÒN ĐỀU

A. Phương pháp :

1.Dùng mối liên hệ giữa dao động điều hoà và chuyển động tròn đều.

+Ta xét:  \(u=U_{0}cos(\omega t+\varphi )\) được biểu diễn bằng OM quay quanh vòng tròn tâm O bán kính U0, quay ngược chiều  kim đồng hồ với tốc độ góc ω ,

+ Có 2 điểm M, N hoạt động tròn đều có hình chiếu lên Ou là u, thì :- N có hình chiếu lên Ou lúc u đang tăng ( thì chọn góc âm phía dưới ) ,- M có hình chiếu lên Ou lúc u đang giảm ( thì chọn góc dương phía trên )

=> vào thời gian t ta xét điện áp u có giá trị u và đang biến hóa :- Nếu u theo chiều âm ( đang giảm ) ta chọn M rồi tính góc. \ ( \ alpha = \ widehat { MOU_ { 0 } } \ )

 -Nếu u theo chiều dương (đang tăng) ta chọn N và tính góc:  \(\alpha =-\widehat{NOU_{0}}\)

2. Dòng điện xoay chiều i = I0cos(2πft + φi)

* Mỗi giây đổi chiều 2 f lần* Nếu cho dòng điện qua bộ phận làm rung dây trong hiện tượng kỳ lạsóng dừng thì dây rung với tần số 2 f

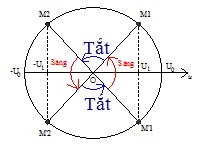
3. Công thức tính thời gian đèn huỳnh quang sáng trong một chu kỳ

Khi đặt điện áp u = U0cos ( ωt + φu ) vào hai đầu bóng đèn, biết đèn chỉ sáng lên khi \ ( \ left | u \ right | \ ) ≥ U1. Gọi ∆ t là khoảng chừng thời hạn đèn sáng trong một chu kỳ luân hồi \ ( \ Delta t = \ frac { 4 \ Delta \ varphi } { \ omega } \ ) Với \ ( \ Delta \ varphi = \ widehat { M_ { 1 } OU_ { 0 } } ; cos \ Delta \ varphi = \ frac { U_ { 1 } } { U_ { 0 } } \ ) ( 0 < ∆ φ < π / 2 )- Thời gian đèn tắt trong một chu kì : \ ( \ Delta t_ { t } = T - \ Delta t_ { s } \ )* ) Trong khoảng chừng thời hạn t = nT :- Thời gian đèn sáng : \ ( t_ { s } = n. \ Delta t_ { s } \ ) ;

 -Thời gian đèn tắt: \(t_{t}=n.\Delta t_{t}=t-t_{s}\)

B.Áp dụng :

Bài  1 : Biểu thức cường độ dòng điện xoay chiều chạy qua một đoạn mạch là \(i=I_{0}cos(100\pi t)(A)\), với I0 > 0 và t tính bằng giây (s). Tính từ lúc 0 s, xác định thời điểm đầu tiên mà dòng điện có cường độ tức thời bằng cường độ hiệu dụng ?

Bài  giải :

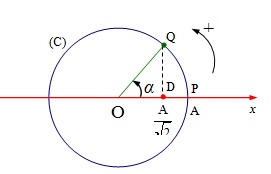
Biểu thức cường độ dòng điện \ ( i = I_ { 0 } cos ( 100 \ pi t ) ( A ) \ ) giống về mặt toán học với biểu thức li độ \ ( x = Acos ( \ omega t ) \ ) của chất điểm dao động cơ điều hoà. Do đó, tính từ lúc 0 s, tìm thời gian tiên phong để dòng điện có cường độ tức thời bằng cường độ hiệu dụng \ ( i = I = I_ { 0 } / \ sqrt { 2 } \ ) cũng giống như tính từ lúc 0 s, tìm thời gian tiên phong để chất điểm dao động cơ điều hoà có li độ \ ( x = A / \ sqrt { 2 } \ ). Vì pha khởi đầu của xê dịch bằng 0, nghĩa là lúc 0 s thì chất điểm đang ở vị trí số lượng giới hạn x = A, nên thời gian cần tìm chính bằng thời hạn ngắn nhất để chất điểm đi từ vị trí số lượng giới hạn x = A đến vị trí có li độ \ ( x = A / \ sqrt { 2 } \ ). Ta sử dụng đặc thù hình chiếu của một chất điểm hoạt động tròn đều lên một đường thẳng nằm trong mặt phẳng quỹ đạo là một giao động điều hoà với cùng chu kì để giải Bài toán này .

Thời gian ngắn nhất để chất điểm giao động điều hoà hoạt động từ vị trí có li độ x = A đến vị trí có li độ \ ( x = A / \ sqrt { 2 } \ ) ( từ P. đến D ) chính bằng thời hạn chất điểm hoạt động tròn đều với cùng chu kì đi từ P. đến Q. theo cung tròn PQ .Tam giác ODQ vuông tại D và có OQ = A, \ ( OD = A / \ sqrt { 2 } \ ) nên ta có : \ ( cos \ alpha = \ frac { OD } { OQ } = \ frac { \ sqrt { 2 } } { 2 } \ )Suy ra : \ ( \ alpha = \ frac { \ pi } { 4 } \ ) radThời gian chất điểm hoạt động tròn đều đi từ P. đến Q. theo cung tròn PQ là : \ ( t = \ frac { \ alpha } { \ omega } = \ frac { \ pi } { 4 } / \ omega = \ frac { 1 } { 4 \ omega } \ )Trong biểu thức của dòng điện, thì tần số góc ω = 100 π rad / s nên ta suy ra tính từ lúc 0 s thì thời gian tiên phong mà dòng điện có cường độ tức thời bằng cường độ hiệu dụng là :\ ( t = \ frac { \ pi } { 4 \ omega } = \ frac { \ pi } { 4.100 \ pi } = \ frac { 1 } { 400 } s \ )

TRĂC NGHIỆM :

Câu 1. Dòng điện xoay chiều qua một đoạn mạch có biểu thức \(i=I_{0}cos(120\pi t-\pi /3)A\). Thời điểm thứ 2009 cường độ dòng điện tức thời bằng cường độ hiệu dụng là:

A. \ ( \ frac { 12049 } { 1440 } s \ ) B. \ ( \ frac { 24097 } { 1440 } s \ ) C. \ ( \ frac { 24113 } { 1440 } s \ ) D. Đáp án khác

Câu  2. Điện áp tức thời giữa hai đầu đoạn mạch \(u=240sin100\pi t(V)\). Thời điểm gần nhất sau đó để điện áp tức thời đạt giá trị 120V là :

A. 1/600 s B. 1/100 s C. 0,02 s D. 1/300 s

DẠNG 3. ĐIỆN LƯỢNG QUA TIẾT DIỆN DÂY DẪN

A. Phương pháp :

 +Điện lượng qua tiết diện S trong thời gian t là q với  :   q = i.t

  +Điện lượng qua tiết diện S trong thời gian từ t1 đến t2  là Δq :   Δq=i.Δt

*)Chú ý :Bấm máy tính phải để ở chế độ rad.

B.Áp dụng :

Câu 1 :Dòng điện xoay chiều i=2sin100πt(A) qua một dây dẫn. Điện lượng chạy qua tiết diện dây trong khoảng thời gian từ 0 đến 0,15s là :

A. 0 B. 4/100 π ( C ) C. 3/100 π ( C ) D. 6/100 π ( C )

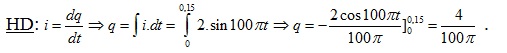
Chọn B

Câu 2 : (Đề 23 cục khảo thí )Dòng điện xoay chiều có biểu thức \(i=2cos100\pi t(A)\) chạy qua dây dẫn. điện lượng chạy qua một tiết điện dây trong khoảng thời gian từ 0 đến  0,15s là :

A. 0 B. \ ( \ frac { 4 } { 100 \ pi } ( C ) \ ) C. \ ( \ frac { 3 } { 100 \ pi } ( C ) \ ) D. \ ( \ frac { 6 } { 100 \ pi } ( C ) \ )

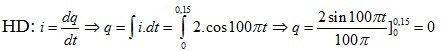
Chọn A

Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:

Luyện Bài tập trắc nghiệm môn Vật lý lớp 12 – Xem ngay

Source: https://vh2.com.vn
Category : Khoa Học