Đồ họa của Tech Insider cho thấy những lục địa sẽ hợp nhất thành một dải đất duy nhất trong vòng 250 triệu năm tới . Bạn đang đọc: Các...
Góc giữa 2 vecto trong không gian: Lý thuyết, bài tập & tài liệu
Trong hình học không gian, bài toán tính góc giữa 2 vecto trong không gian là một bài toán khó trong chương trình toán lớp 12. Nó phụ thuộc vào nhiều kiến thức khác nhau liên quan đến mặt phẳng, thiết diện. Hiểu được những khó khăn khi làm dạng bài này, Verbalearn sẽ giúp bạn hiểu rõ hơn ngay trong bài viết dưới đây.
Định nghĩa góc giữa hai vecto trong không gian
Góc giữa hai vecto trong không gian có cùng định nghĩa với góc giữa hai vecto trong mặt phẳng. Ta có 2 định lý như sau :
- Góc không xác định nếu tồn tại 1 vecto không (Có thể nói góc bằng 0)
- Cả 2 vecto đều khác không, tiến hành đưa về chung gốc để có thể tính toán
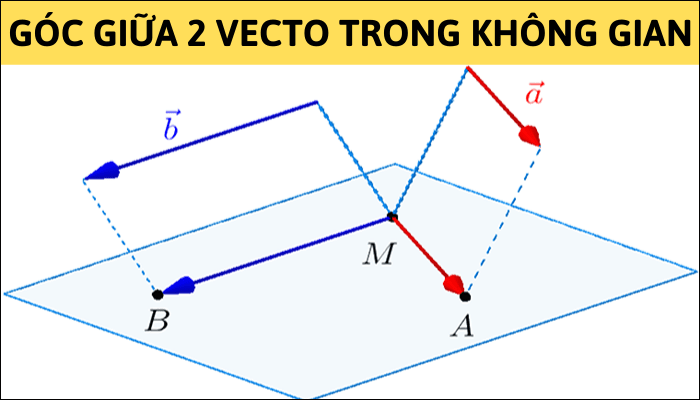
Tính chất góc giữa hai vecto
Gọi $\alpha $ là góc giữa hai vecto bất kì trong không gian. Ta có các tính chất sau:
- $\alpha = {0^0}$ khi hai vecto đó cùng chiều
- $\alpha = {90^0}$ khi hai vecto vuông góc
- $\alpha = {180^0}$ khi hai vecto ngược chiều
Công thức tính góc giữa hai vecto
Áp dụng công thức tính góc giữa hai vecto giúp bạn hoàn toàn có thể tính được những bài toán cơ bản một cách nhanh gọn nhất. Dưới đây là công thức tổng quát ứng dụng cho những vecto trong không gian. Để tính được góc giữa hai vecto, sử dụng công thức sau để tính cosin của góc rồi từ đó đổi thành số đo nếu đề bài nhu yếu .
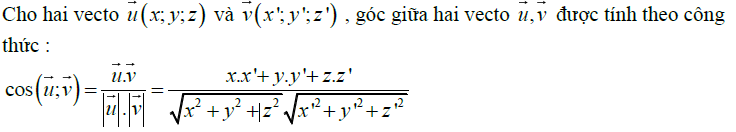
Lưu ý
Góc giữa hai vectơ thuộc khoảng chừng : $ { \ rm { [ } } { 0 ^ 0 } ; { 180 ^ 0 } { \ rm { ] } } $
Tích vô hướng của hai vecto trong không gian
Tích vô hướng của hai vecto trong không gian là một kỹ năng và kiến thức quan trọng. Với công thức tích vô hướng, bạn không chỉ tính được cosin của góc mà còn xác lập được nhiều yếu tố khác .
1. Góc giữa hai vecto chung gốc
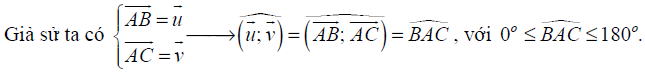
2. Tích vô hướng của hai vecto trong không gian
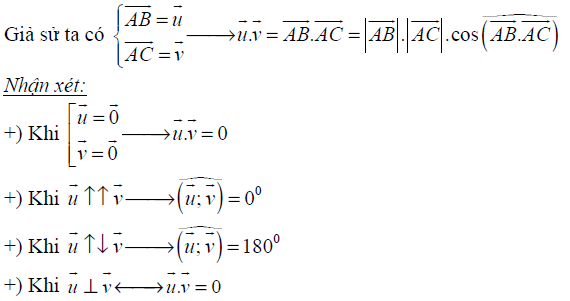
3. Tìm hiểu các ví dụ
Bài toán 1: Tính góc tạo bởi vecto là các cạnh của một tứ diện đều.
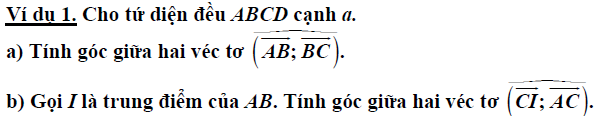
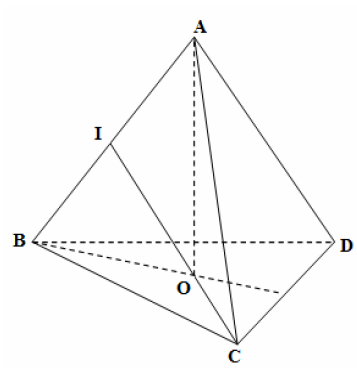


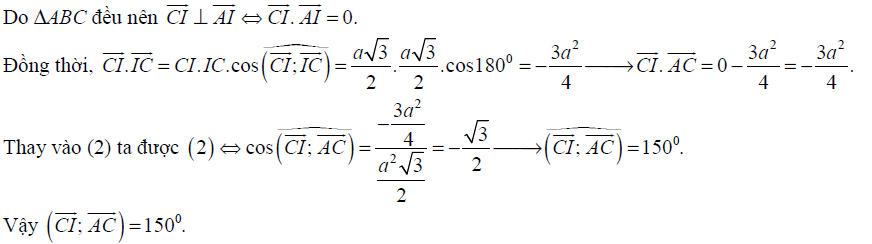
Trên đây là bài toán cơ bản nhất về tính góc giữa hai vecto. Với bài toán này, bạn cần chú ý quan tâm những đặc thù của tứ diện đều để không bỏ sót qua những dữ kiện. Tiếp theo tất cả chúng ta cùng đến với một bài toán tính góc giữa hai vecto với đề bài cho trước là hình chóp có nhiều yếu tố vuông góc .

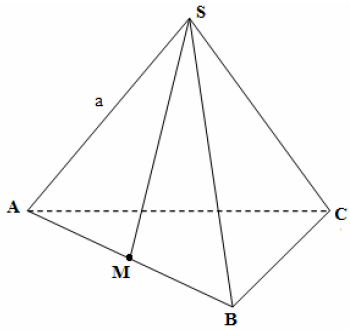

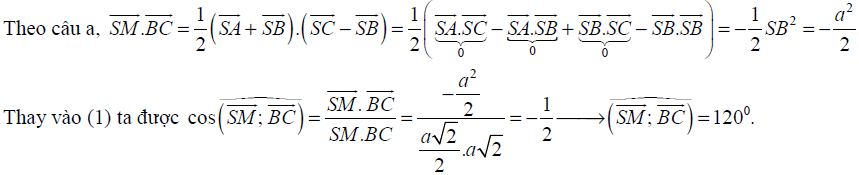
Xem thêm: Keanu Reeves – Wikipedia tiếng Việt
Tính góc giữa hai vecto bằng Casio
Từ khi toán học chuyển sang thi trắc nghiệm thì việc vận dụng máy tính Casio vào giải bài tập là điều thiết yếu. Không chỉ riêng đại số, mà ngay cả hình học việc vận dụng máy tính cầm tay vẫn hiệu suất cao. Lưu ý rằng, để sử dụng thuần thục casio thứ nhất bạn hãy nắm vững triết lý để không làm mất thực chất của môn học .
1. Các lệnh nhập Casio có liên quan đến dạng bài
- Lệnh đăng nhập khi làm dạng toán về vecto: MODE 8
- Nhập thông số vecto: MODE 8 1 1
- Tính tích vô hướng của 2 vecto: VectoA SHIFT 5 7 VectoB
- Tính tích có hướng của hai vecto: VectoA x VectoB
- Lệnh giá trị tuyệt đối: SHIFT HYP
- Lệnh tính độ lớn một vecto: SHIFT HYP
- Lệnh dò nghiệm của bất phương trình: MODE 7
- Lệnh dò nghiệm của phương trình: SHIFT SOLVE
Sau khi tìm hiểu và khám phá những lệnh nhập Casio có tương quan đến vecto. Để tính góc bằng Casio, cách nhanh nhất là bạn hãy cùng theo dõi những ví dụ sau và thực thi lại .
2. Các ví dụ minh họa
Câu 1: Tính góc giữa hai vecto cho trước đã có tọa độ
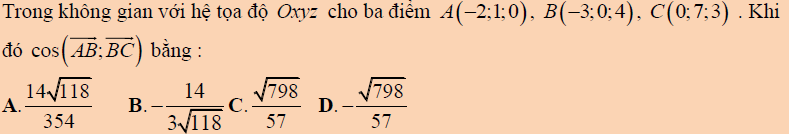
Nhập hai vecto USD ( \ overrightarrow { AB } ; \ overrightarrow { BC } ) USD vào máy tính :

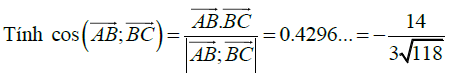
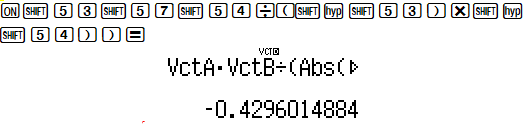
→ Đáp số chính là là câu B
Câu 2: Tìm điều kiện của tham số để góc giữa hai vecto thỏa mãn yêu cầu cho trước
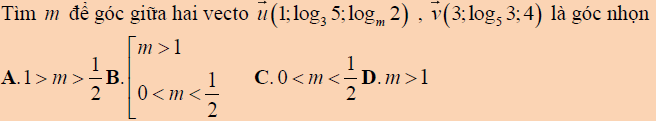
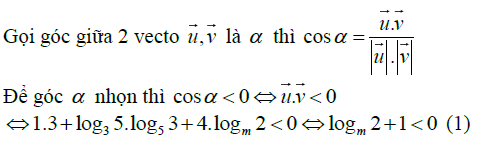

![]()
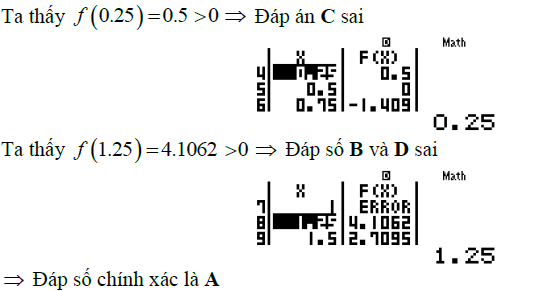
Câu 3: Tìm tham số m để thỏa mãn số đo góc
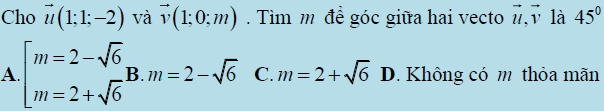
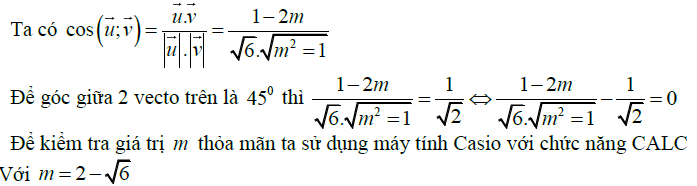
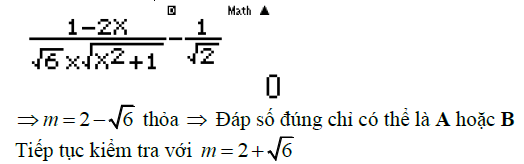
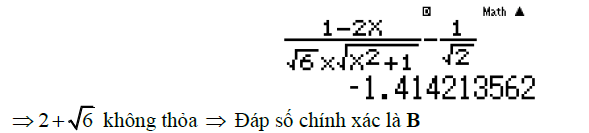
Trên đây là hàng loạt những kiến thức và kỹ năng về góc giữa hai vecto trong không gian và 1 số ít chiêu thức tính. Ngoài kĩ năng sử dụng máy tính, để làm thuần thục dạng bài tập này học viên cần hiểu thực chất vecto trong không gian, những công thức lượng giác cơ bản. Cuối cùng, Verbalearn chúc những em học tốt và học thật chắc như đinh những dạng bài tập này .
Source: https://vh2.com.vn
Category : Trái Đất





