Lý thuyết, bài tập về Góc và khoảng cách trong không gian có đáp án

Tailieumoi. vn xin ra mắt đến các quý thầy cô, các em học viên đang trong quy trình ôn tập tài liệu bài tập Góc và khoảng cách trong không gian Toán lớp 12, tài liệu gồm có 47 trang, tuyển chọn 49 bài tập Góc và khoảng cách trong không gian vừa đủ kim chỉ nan, giải pháp giải cụ thể và giải thuật, giúp các em học viên có thêm tài liệu tìm hiểu thêm trong quy trình ôn tập, củng cố kiến thức và kỹ năng và sẵn sàng chuẩn bị cho kì thi tốt nghiệp trung học phổ thông môn Toán sắp tới. Chúc các em học viên ôn tập thật hiệu suất cao và đạt được hiệu quả như mong đợi .
Tài liệu Lý thuyết, bài tập về Góc và khoảng cách trong không gian có đáp án gồm các nội dung sau :

A. Góc trong không gian

– Tóm tắt ngắn gọn phương pháp giải các dạng bài tập và 24 câu hỏi trắc nghiệm có đáp án và lời giải chi tiết

B. Khoảng cách trong không gian

– Tóm tắt ngắn gọn chiêu thức giải các dạng bài tập và 25 câu hỏi trắc nghiệm có đáp án và giải thuật chi tiết cụ thể
Mời các quý thầy cô và các em học viên cùng tìm hiểu thêm và tải về cụ thể tài liệu dưới đây :

Vấn đề 7 GÓC – KHOẢNG CÁCH

A. GÓC TRONG KHÔNG GIAN

1. Góc giữa đường thẳng a và đường thẳng b

Phương pháp 1. Sử dụng song song, tức dựng đường thẳng c // b  và c cắt a.

Khi đó a ; b ^ = a ; c ^ = α như hình vẽ .
Sử dụng hệ thức lượng trong tam giác vuông hoặc định lí hàm số sin, côsin để tìm góc α

Phương pháp 2. Sử dụng tích vô hướng, nghĩa là cosa;b=cosa→;b→=a→.b→a→b→

Khi đó, ta cần chèn điểm tương thích để tính tích vô hướng .

Phương pháp 3. Ghép vào hệ trục tọa độ Oxyz

Lưu ý: Góc giữa hai đường thẳng là góc nhọn, còn góc giữa hai véctơ là góc nhọn hoặc góc tù. Nghĩa là
nếu tính a;b^=α≤90° thì góc giữa a b, là α, còn nếu tính a;b^=α>90° thì góc giữa hai
đường thẳng a;b^=180°-α

2. Góc giữa đường thẳng AB và mặt phẳng (P)

Cần nhớ : “ Góc giữa đường thẳng và mặt phẳng là góc tạo bởi nó và hình chiếu của nó lên mặt phẳng ” .

Phương pháp 1. Sử dụng hình học 11.

B. 1. Tìm AB∩(P)=A (1)

B. 2. Tìm hình chiếu của B lên mặt phẳng ( P)

Đặt câu hỏi và vấn đáp : “ Đường nào qua B và vuông góc với ( P. ) ? “ ( có sẵn hoặc dựng thêm )
Trả lời : BH ⊥ ( P. ) tại H ( 2 )
Từ ( 1 ), ( 2 ), suy ra AH là hình chiếu của AB lên mặt phẳng ( P. )
Do đó góc giữa đường thẳng AB và mp ( P. ) là góc giữa AB và AH, chính là góc BAH ^

B. 3. Sử dụng hệ thức lượng trong tam giác vuông hoặc định lí hàm số côsin hoặc định lí hàm sin trong tam
giác thường để suy ra góc BAH^

Phương pháp 2. Ghép vào hệ trục tọa độ Oxyz.

3. Góc giữa mặt phẳng (P) và mặt phẳng (Q)

Phương pháp 1. Dựa vào định nghĩa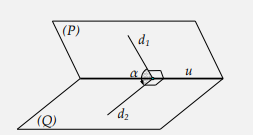

Ta có: P∩Q=uu⊥d1⊂Pu⊥d2⊂Q⇒P;Q^=d1;d2^=α

Phhương pháp 2. Tìm hai đường thẳng d1 và d2 lần lượt vuông góc với mặt phẳng (P) và mặt phẳng (Q)

Góc giữa hai mặt phẳng là góc giữa d1 và d2

Phương pháp 3. Sử dụng công thức hình chiếu S’=S.cosα

Xem thêm

Source: https://vh2.com.vn
Category : Trái Đất