Chuyên đề hình học giải tích trong không gian Oxyz

Tailieumoi. vn xin ra mắt đến những quý thầy cô, những em học viên đang trong quy trình ôn tập tài liệu Chuyên đề hình học giải tích trong không gian Oxyz, tài liệu gồm có 60 trang. Tài liệu được tổng hợp từ những tài liệu ôn thi hay nhất giúp những em học viên có thêm tài liệu tìm hiểu thêm trong quy trình ôn tập, củng cố kiến thức và kỹ năng và sẵn sàng chuẩn bị cho kỳ thi sắp hới. Chúc những em học viên ôn tập thật hiệu suất cao và đạt được hiệu quả như mong đợi .
Mời những quý thầy cô và những em học viên cùng tìm hiểu thêm và tải về cụ thể tài liệu dưới đây

Chuyên đề hình học giải tích trong không gian Oxyz

Bài 1: Mở đầu

I. Vec tơ trong không gian

1. Định nghĩa và những phép toán
Định nghĩa, đặc thù, những phép toán về vectơ trong không gian được thiết kế xây dựng trọn vẹn tựa như như trong mặt phẳng .
Lưu ý :
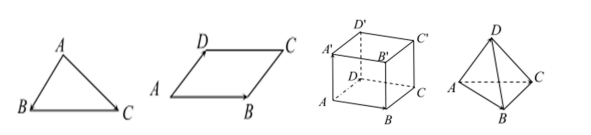
Qui tắc ba điểm : Cho ba điểm A, B, C bất kể, ta có : \ [ \ overrightarrow { AB } + \ overrightarrow { BC } = \ overrightarrow { AC } \ ]
Qui tắc hình bình hành : Cho hình bình hành ABCD, ta có : \ [ \ overrightarrow { AB } + \ overrightarrow { AD } = \ overrightarrow { AC } \ ]
Qui tắc hình hộp : Cho hình hộp ABCD.A ′ B ′ C ′ D ′, ta có : \ [ \ overrightarrow { AB } + \ overrightarrow { AD } + \ overrightarrow { AA ‘ } = \ overrightarrow { AC ‘ } \ ]
Hệ thức trung điểm đoạn thẳng : Cho I là trung điểm của đoạn thẳng AB, O tuỳ ý .
Ta có : \ [ \ overrightarrow { IA } + \ overrightarrow { IB } = \ overrightarrow 0 \ ] ; \ [ \ overrightarrow { OA } + \ overrightarrow { OB } = 2 \ overrightarrow { OI } \ ]
Hệ thức trọng tâm tam giác : Cho G là trọng tâm của tam giác ABC, O tuỳ ý .
Ta có : \ [ \ overrightarrow { GA } + \ overrightarrow { GB } + \ overrightarrow { GC } = \ overrightarrow 0 \ ] ; \ [ \ overrightarrow { OA } + \ overrightarrow { OB } + \ overrightarrow { OC } = 3 \ overrightarrow { OG } \ ]
Hệ thức trọng tâm tứ diện : Cho G là trọng tâm của tứ diện ABCD, O tuỳ ý .
Ta có : \ [ \ overrightarrow { GA } + \ overrightarrow { GB } + \ overrightarrow { GC } + \ overrightarrow { GD } = \ overrightarrow 0 \ ] ; \ [ \ overrightarrow { OA } + \ overrightarrow { OB } + \ overrightarrow { OC } + \ overrightarrow { OD } = 4 \ overrightarrow { OG } \ ]
Điều kiện hai vectơ cùng phương : \ [ \ overrightarrow a \ ] và \ [ \ overrightarrow b \ ] cùng phương ( \ [ \ overrightarrow a \ ne \ overrightarrow 0 \ ] ) \ [ \ Leftrightarrow \ exists ! k \ in R : \ overrightarrow b = k \ overrightarrow a \ ]
Điểm M chia đoạn thẳng AB theo tỉ số k ( k ≠ 1 ), O tuỳ ý .
Ta có : \ [ \ overrightarrow { MA } = k \ overrightarrow { MB } \ ] ; \ [ \ overrightarrow { OM } = \ frac { { \ overrightarrow { OA } – k \ overrightarrow { OB } } } { { 1 – k } } \ ]
2. Sự đồng phẳng của ba vectơ
Ba vectơ được gọi là đồng phẳng nếu những giá của chúng cùng song song với một mặt phẳng .
Điều kiện để ba vectơ đồng phẳng : Cho ba vectơ \ [ \ overrightarrow a, \ overrightarrow b, \ overrightarrow c \ ], trong đó \ [ \ overrightarrow a \ ] và \ [ \ overrightarrow b \ ] không cùng phương. Khi đó : \ [ \ overrightarrow a, \ overrightarrow b, \ overrightarrow c \ ] đồng phẳng \ [ \ Leftrightarrow \ exists ! m, n \ in R : \ overrightarrow c = m \ overrightarrow a + n \ overrightarrow b \ ]
Cho ba vectơ \ [ \ overrightarrow a, \ overrightarrow b, \ overrightarrow c \ ] không đồng phẳng, \ [ \ overrightarrow x \ ] tuỳ ý .
Khi đó : \ [ \ Leftrightarrow \ exists ! m, n, p \ in R : \ overrightarrow x = m \ overrightarrow a + n \ overrightarrow b + p \ overrightarrow c \ ]
3. Tích vô hướng của hai vectơ
Góc giữa hai vectơ trong không gian :
\ [ \ overrightarrow { AB } = \ overrightarrow u, \ overrightarrow { AC } = \ overrightarrow v \ Rightarrow \ left ( { \ overrightarrow u, \ overrightarrow v } \ right ) = \ widehat { BAC } \ ] \ [ ( { 0 ^ 0 } \ le \ widehat { BAC } \ le { 180 ^ 0 } ) \ ]
Tích vô hướng của hai vectơ trong không gian :
Cho \ [ \ overrightarrow u, \ overrightarrow v \ ne \ overrightarrow 0 \ ]. Khi đó : \ [ \ overrightarrow u. \ overrightarrow v = \ left | { \ overrightarrow u } \ right |. \ left | { \ overrightarrow v } \ right |. \ cos \ left ( { \ overrightarrow u, \ overrightarrow v } \ right ) \ ]
Với \ [ \ overrightarrow u = \ overrightarrow 0 \ ] hoặc \ [ \ overrightarrow v = \ overrightarrow 0 \ ]. Qui ước : \ [ \ overrightarrow u. \ overrightarrow v = 0 \ ]
\ [ \ overrightarrow u \ bot \ overrightarrow v \ Leftrightarrow \ overrightarrow u. \ overrightarrow v = 0 \ ]
\ [ \ left | { \ overrightarrow u } \ right | = \ sqrt { \ overrightarrow { { u ^ 2 } } } \ ]

II. Hệ tọa độ trong không gian

1. Hệ tọa độ Đêcac vuông góc trong không gian :
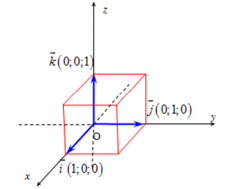
Cho ba trục Ox, Oy, Oz vuông góc với nhau từng đôi một và chung một điểm gốc O. Gọi \ [ \ overrightarrow i, \ overrightarrow j, \ overrightarrow k \ ] là những vectơ đơn vị chức năng, tương ứng trên những trục Ox, Oy, Oz. Hệ ba trục như vậy gọi là hệ tọa độ Đêcac vuông góc Oxyz hoặc đơn thuần là hệ tọa độ Oxyz .
Chú ý : \ [ \ overrightarrow { { i ^ 2 } } = \ overrightarrow { { j ^ 2 } } = \ overrightarrow { { k ^ 2 } } = 1 \ ] và \ [ \ overrightarrow i. \ overrightarrow j = \ overrightarrow i. \ overrightarrow k = \ overrightarrow k. \ overrightarrow j = 0 \ ]
2. Tọa độ của vecto :
a. Định nghĩa : \ [ \ overrightarrow u = ( x ; y ; z ) \ Leftrightarrow \ overrightarrow u = x \ overrightarrow i + y \ overrightarrow j + z \ overrightarrow k \ ]
b. Tính chất : Cho \ [ \ overrightarrow a = ( { a_1 } ; { a_2 } ; { a_3 } ) \ ], \ [ \ overrightarrow b = ( { b_1 } ; { b_2 } ; { b_3 } ) \ ], \ [ k \ in R \ ]
\ [ \ overrightarrow a \ pm \ overrightarrow b = ( { a_1 } \ pm { b_1 } ; { a_2 } \ pm { b_2 } ; { a_3 } \ pm { b_3 } ) \ ]
\ [ k \ overrightarrow a = ( k { a_1 } ; k { a_2 } ; k { a_3 } ) \ ]
\ [ \ overrightarrow a = \ overrightarrow b \ Leftrightarrow \ left \ { { \ begin { array } { * { 20 } { c } } { { a_1 } = { b_1 } } \ \ { { a_2 } = { b_2 } } \ \ { { a_3 } = { b_3 } } \ end { array } } \ right. \ ]
\ [ \ overrightarrow 0 = ( 0 ; 0 ; 0 ) \ ], \ [ \ overrightarrow i = ( 1 ; 0 ; 0 ) \ ], \ [ \ overrightarrow j = ( 0 ; 1 ; 0 ) \ ], \ [ \ overrightarrow k = ( 0 ; 0 ; 1 ) \ ]
\ [ \ overrightarrow a \ ], \ [ \ overrightarrow b \ ] cùng phương \ [ \ overrightarrow b \ ne \ overrightarrow 0 \ ] \ [ \ Leftrightarrow \ overrightarrow a = k. \ overrightarrow b \ ] ( \ [ k \ in R \ ] )
\ [ \ Leftrightarrow \ left \ { { \ begin { array } { * { 20 } { c } } { { a_1 } = k { b_1 } } \ \ { { a_2 } = k { b_2 } } \ \ { { a_3 } = k { b_3 } } \ end { array } } \ right. \ Leftrightarrow \ frac { { { a_1 } } } { { { b_1 } } } = \ frac { { { a_2 } } } { { { b_2 } } } = \ frac { { { a_3 } } } { { { b_3 } } } \ ] \ [ ( { b_1 } ; { b_2 } ; { b_3 } \ ne 0 ) \ ]
\ [ \ overrightarrow a. \ overrightarrow b = { a_1 }. { b_1 } + { a_2 }. { b_2 } + { a_3 }. { b_3 } \ ]
\ [ \ overrightarrow a \ bot \ overrightarrow b \ Leftrightarrow { a_1 }. { b_1 } + { a_2 }. { b_2 } + { a_3 }. { b_3 } = 0 \ ]
\ [ \ overrightarrow { { a ^ 2 } } = a_1 ^ 2 + a_2 ^ 2 + a_3 ^ 2 \ ]
\ [ \ left | { \ overrightarrow a } \ right | = \ sqrt { a_1 ^ 2 + a_2 ^ 2 + a_3 ^ 2 } \ ]
\ [ \ cos \ left ( { \ overrightarrow a ; \ overrightarrow b } \ right ) = \ frac { { \ overrightarrow a. \ overrightarrow b } } { { \ left | { \ overrightarrow a } \ right |. \ left | { \ overrightarrow b } \ right | } } = \ frac { { { a_1 }. { b_1 } + { a_2 }. { b_2 } + { a_3 }. { b_3 } } } { { \ sqrt { a_1 ^ 2 + a_2 ^ 2 + a_3 ^ 2 }. \ sqrt { b_1 ^ 2 + b_2 ^ 2 + b_3 ^ 2 } } } \ ] ( với \ [ \ overrightarrow a, \ overrightarrow b \ ne \ overrightarrow 0 \ ] )

3. Tọa độ của điểm
a. Định nghĩa : \ [ M ( x ; y ; z ) \ ] \ [ \ Leftrightarrow \ overrightarrow { OM } = x \ overrightarrow i + y \ overrightarrow j + z \ overrightarrow k \ ] ( x : hoành độ, y : tung độ, z : cao độ )
Chú ý :
\ [ M \ in ( Oxy ) \ Leftrightarrow z = 0 \ ] ; \ [ M \ in ( Oyz ) \ Leftrightarrow x = 0 \ ] ; \ [ M \ in ( Oxz ) \ Leftrightarrow y = 0 \ ]
\ [ M \ in Ox \ Leftrightarrow y = z = 0 \ ] ; \ [ M \ in Oy \ Leftrightarrow x = z = 0 \ ] ; \ [ M \ in Oz \ Leftrightarrow x = y = 0 \ ]
b. Tính chất : Cho \ [ A ( { x_A } ; { y_A } ; { z_A } ) \ ], \ [ B ( { x_B } ; { y_B } ; { z_B } ) \ ]
\ [ \ overrightarrow { AB } = ( { x_B } – { x_A } ; { y_B } – { y_A } ; { z_B } – { z_A } ) \ ]
\ [ AB = \ sqrt { { { ( { x_B } – { x_A } ) } ^ 2 } + { { ( { y_B } – { y_A } ) } ^ 2 } + { { ( { z_B } – { z_A } ) } ^ 2 } } \ ]
Tọa độ điểm M chia đoạn AB theo tỉ số k ( k ≠ 1 ) :
\ [ M ( \ frac { { { x_A } – k { x_B } } } { { 1 – k } } ; \ frac { { { y_A } – k { y_B } } } { { 1 – k } } ; \ frac { { { z_A } – k { z_B } } } { { 1 – k } } ) \ ]
Tọa độ trung điểm M là trung điểm của đoạn AB :
\ [ M ( \ frac { { { x_A } + { x_B } } } { 2 } ; \ frac { { { y_A } + { y_B } } } { 2 } ; \ frac { { { z_A } + { z_B } } } { 2 } ) \ ]
Tọa độ trọng tâm G của tam giác ABC :
\ [ G = ( \ frac { { { x_A } + { x_B } + { x_C } } } { 3 } ; \ frac { { { y_A } + { y_B } + { y_C } } } { 3 } ; \ frac { { { z_A } + { z_B } + { z_C } } } { 3 } ) \ ]
Tọa độ trọng tâm G của tứ diện ABCD : \ [ G = ( \ frac { { { x_A } + { x_B } + { x_C } + { x_D } } } { 4 } ; \ frac { { { y_A } + { y_B } + { y_C } + { y_D } } } { 4 } ; \ frac { { { z_A } + { z_B } + { z_C } + { z_D } } } { 4 } ) \ ]

4. Tích có hướng của hai vectơ : ( Chương trình nâng cao )
a. Định nghĩa : Cho \ [ \ overrightarrow a = ( { a_1 } ; { a_2 } ; { a_3 } ), \ overrightarrow b = ( { b_1 } ; { b_2 } ; { b_3 } ) \ ]
\ [ \ begin { array } { l } \ left [ { \ overrightarrow a, \ overrightarrow b } \ right ] = \ overrightarrow a \ wedge \ overrightarrow b = \ left ( { \ left | { \ begin { array } { * { 20 } { c } } { { a_2 } } và { { a_3 } } \ \ { { b_2 } } và { { b_3 } } \ end { array } } \ right | ; \ left | { \ begin { array } { * { 20 } { c } } { { a_3 } } và { { a_1 } } \ \ { { b_3 } } và { { b_1 } } \ end { array } } \ right | ; \ left | { \ begin { array } { * { 20 } { c } } { { a_1 } } và { { a_2 } } \ \ { { b_1 } } và { { b_2 } } \ end { array } } \ right | } \ right ) \ \ = \ left ( { { a_2 } { b_3 } – { a_3 } { b_2 } ; { a_3 } { b_1 } – { a_1 } { b_3 } ; { a_1 } { b_2 } – { a_2 } { b_1 } } \ right ) \ end { array } \ ]
Chú ý : Tích có hướng của hai vectơ là một vectơ, tích vô hướng của hai vectơ là một số ít .
b. Tính chất :
\ [ \ left [ { \ overrightarrow i. \ overrightarrow j } \ right ] = \ overrightarrow k \ ]
\ [ \ left [ { \ overrightarrow j. \ overrightarrow k } \ right ] = \ overrightarrow i \ ]
\ [ \ left [ { \ overrightarrow k. \ overrightarrow j } \ right ] = \ overrightarrow j \ ]
\ [ \ left [ { \ overrightarrow a. \ overrightarrow b } \ right ] \ bot \ overrightarrow a \ ]
\ [ \ left [ { \ overrightarrow a. \ overrightarrow b } \ right ] \ bot \ overrightarrow b \ ]
\ [ \ left | { \ left [ { \ overrightarrow a. \ overrightarrow b } \ right ] } \ right | = \ left | { \ overrightarrow a } \ right |. \ left | { \ overrightarrow b } \ right |. \ sin \ left ( { \ overrightarrow a, \ overrightarrow b } \ right ) \ ]
\ [ \ overrightarrow a \ ], \ [ \ overrightarrow b \ ] cùng phương \ [ \ Leftrightarrow \ left [ { \ overrightarrow a. \ overrightarrow b } \ right ] = \ overrightarrow 0 \ ]
c ) Ứng dụng của tích có hướng :

Điều kiện đồng phẳng của ba vectơ: \[\overrightarrow a ,\overrightarrow b \] và \[\overrightarrow c \]đồng phẳng \[ \Leftrightarrow \left[ {\overrightarrow a ,\overrightarrow b } \right].\overrightarrow c  = 0\]

Diện tích hình bình hành ABCD : \ [ { S_ { ABCD } } = \ left | { \ left [ { \ overrightarrow { AB }, \ overrightarrow { AD } } \ right ] } \ right | \ ]
Diện tích tam giác ABC : \ [ { S_ { \ Delta ABC } } = \ frac { 1 } { 2 } \ left | { \ left [ { \ overrightarrow { AB }, \ overrightarrow { AC } } \ right ] } \ right | \ ]
Thể tích khối hộp ABCD.A ′ B ′ C ′ D ′ : \ [ { V_ { ABCD.A ‘ B’C ‘ D ‘ } } = \ left | { \ left [ { \ overrightarrow { AB }, \ overrightarrow { AC } } \ right ]. \ overrightarrow { AA ‘ } } \ right | \ ]
Thể tı ́ ch tứ diện ABCD : \ [ { V_ { ABCD } } = \ frac { 1 } { 6 } \ left | { \ left [ { \ overrightarrow { AB }, \ overrightarrow { AC } } \ right ]. \ overrightarrow { AD } } \ right | \ ]
Chú ý :
Tích vô hướng của hai vectơ thường sử dụng để chứng tỏ hai đường thẳng vuông góc, tính góc giữa hai đường thẳng .
Tích có hướng của hai vectơ thường sử dụng để tính diện tích quy hoạnh tam giác ; tính thể tích khối tứ diện, thể tích hình hộp ; chứng tỏ những vectơ đồng phẳng – không đồng phẳng, chứng tỏ những vectơ cùng phương .
\ [ \ overrightarrow a \ bot \ overrightarrow b \ Leftrightarrow \ overrightarrow a. \ overrightarrow b = 0 \ ]
\ [ \ overrightarrow a \ ], \ [ \ overrightarrow b \ ] cùng phương \ [ \ Leftrightarrow \ left [ { \ overrightarrow a. \ overrightarrow b } \ right ] = \ overrightarrow 0 \ ]
\ [ \ overrightarrow a, \ overrightarrow b \ ] và \ [ \ overrightarrow c \ ] đồng phẳng \ [ \ Leftrightarrow \ left [ { \ overrightarrow a, \ overrightarrow b } \ right ]. \ overrightarrow c = 0 \ ]
5. Phương trình mặt cầu :
Phương trình mặt cầu ( S ) tâm I ( a ; b ; c ), nửa đường kính R : \ [ { ( x – a ) ^ 2 } + { ( y – b ) ^ 2 } + { ( z – c ) ^ 2 } = { R ^ 2 } \ ]
Phương trình \ [ { x ^ 2 } + { y ^ 2 } + { z ^ 2 } + 2 ax + 2 by + 2 cz + d = 0 \ ] với \ [ { a ^ 2 } + { b ^ 2 } + { c ^ 2 } + d > 0 \ ] là phương trình mặt cầu tâm I ( – a ; – b ; – c ) và nửa đường kính \ [ R = \ sqrt { { a ^ 2 } + { b ^ 2 } + { c ^ 2 } + d } \ ] .

Bài tập cơ bản

Bài 1. Cho ba vecto \ [ \ overrightarrow a, \ overrightarrow b, \ overrightarrow c \ ]. Tìm m, n để \ [ \ overrightarrow c = \ left [ { \ overrightarrow a, \ overrightarrow b } \ right ] \ ] :
a. \ [ \ overrightarrow a = ( 3 ; – 1 ; – 2 ), \ overrightarrow b = ( 1 ; 2 ; m ), \ overrightarrow c = ( 5 ; 1 ; 7 ) \ ]
b. \ [ \ overrightarrow a = ( 6 ; – 2 ; m ), \ overrightarrow b = ( 5 ; n ; – 3 ), \ overrightarrow c = ( 6 ; 33 ; 10 ) \ ]
Bài 2. Xét sự đồng phẳng của ba vectơ \ [ \ overrightarrow a, \ overrightarrow b, \ overrightarrow c \ ] trong mỗi trường hợp sau đây :
a. \ [ \ overrightarrow a = ( 1 ; – 1 ; 1 ), \ overrightarrow b = ( 0 ; 1 ; 2 ), \ overrightarrow c = ( 4 ; 2 ; 3 ) \ ]
b. \ [ \ overrightarrow a = ( 4 ; 3 ; 4 ), \ overrightarrow b = ( 2 ; – 1 ; 2 ), \ overrightarrow c = ( 1 ; 2 ; 1 ) \ ]
c. \ [ \ overrightarrow a = ( – 3 ; 1 ; – 2 ), \ overrightarrow b = ( 1 ; 1 ; 1 ), \ overrightarrow c = ( – 2 ; 2 ; 1 ) \ ]
d. \ [ \ overrightarrow a = ( 4 ; 2 ; 5 ), \ overrightarrow b = ( 3 ; 1 ; 3 ), \ overrightarrow c = ( 2 ; 0 ; 1 ) \ ]
Bài 3. Tìm m để 3 vectơ \ [ \ overrightarrow a, \ overrightarrow b, \ overrightarrow c \ ] đồng phẳng :
a. \ [ \ overrightarrow a = ( 1 ; m ; 2 ), \ overrightarrow b = ( m + 1 ; 2 ; 1 ), \ overrightarrow c = ( 0 ; m – 2 ; 2 ) \ ]
b. \ [ \ overrightarrow a = ( 2 m + 1 ; 1 ; 2 m – 1 ), \ overrightarrow b = ( m + 1 ; 2 ; m + 2 ), \ overrightarrow c = ( 2 m ; m + 1 ; 2 ) \ ]
Bài 4. Cho những vectơ \ [ \ overrightarrow a, \ overrightarrow b, \ overrightarrow c, \ overrightarrow u \ ]. Chứng minh ba vectơ \ [ \ overrightarrow a, \ overrightarrow b, \ overrightarrow c \ ] không đồng phẳng. Biểu diễn vecto \ [ \ overrightarrow u \ ] theo những vecto \ [ \ overrightarrow a, \ overrightarrow b, \ overrightarrow c \ ] :
a. \ [ \ left \ { { \ begin { array } { * { 20 } { c } } { \ overrightarrow a = ( 2 ; 1 ; 0 ), \ overrightarrow b = ( 1 ; – 1 ; 2 ), \ overrightarrow c = ( 2 ; 2 ; – 1 ) } \ \ { \ overrightarrow u = ( 3 ; 7 ; – 7 ) } \ end { array } } \ right. \ ]
b. \ [ \ left \ { { \ begin { array } { * { 20 } { c } } { \ overrightarrow a = ( 1 ; – 7 ; 9 ), \ overrightarrow b = ( 3 ; – 6 ; 1 ), \ overrightarrow c = ( 2 ; 1 ; – 7 ) } \ \ { \ overrightarrow u = ( – 4 ; 13 ; – 6 ) } \ end { array } } \ right. \ ]
Bài 5. Chứng tỏ bốn vecto \ [ \ overrightarrow a, \ overrightarrow b, \ overrightarrow c, \ overrightarrow d \ ] đồng phẳng :
a. \ [ \ overrightarrow a = ( – 2 ; – 6 ; 1 ), \ overrightarrow b = ( 4 ; – 3 ; – 2 ), \ overrightarrow c = ( – 4 ; – 2 ; – 2 ), \ overrightarrow d = ( – 2 ; – 11 ; 1 ) \ ]
b. \ [ \ overrightarrow a = ( 2 ; 6 ; – 1 ), \ overrightarrow b = ( 2 ; 1 ; – 1 ), \ overrightarrow c = ( – 4 ; 3 ; 2 ), \ overrightarrow d = ( 2 ; 11 ; – 1 ) \ ]
Bài 6. Cho ba vectơ \ [ \ overrightarrow a, \ overrightarrow b, \ overrightarrow c \ ] không đồng phẳng và vectơ \ [ \ overrightarrow d \ ]. Chứng minh bộ ba vectơ sau không đồng phẳng :
a. \ [ \ overrightarrow b, \ overrightarrow c, \ overrightarrow d = m \ overrightarrow a + n \ overrightarrow b \ ] ( với m, n ≠ 0 )
b. \ [ \ overrightarrow a, \ overrightarrow c, \ overrightarrow d = m \ overrightarrow a + n \ overrightarrow b \ ] ( với m, n ≠ 0 )
Bài 7. Cho điểm M. Tìm tọa độ hình chiếu vuông góc của điểm M :
Trên những mặt phẳng tọa độ : Oxy, Oxz, Oyz
Trên những trục tọa độ : Ox, Oy, Oz
a. M ( 1 ; 2 ; 3 )
b. M ( 3 ; − 1 ; 2 )
c. M − 1 ; 1 ; − 3 )
d. M ( 1 ; 2 ; − 1 )
Bài 8. Cho điểm M. Tìm tọa độ của điểm M ′ đối xứng với điểm M :
Qua gốc toạ độ
Qua mp ( Oxy )
Qua trục Oy
a. M ( 1 ; 2 ; 3 )
b. M ( 3 ; − 1 ; 2 )
c. M ( − 1 ; 1 ; − 3 )
d. M ( 1 ; 2 ; − 1 )
Bài 9. Xét tính thẳng hàng của những bộ ba điểm sau :
a ) A ( 1 ; 3 ; 1 ), B ( 0 ; 1 ; 2 ), C ( 0 ; 0 ; 1 )
b. A ( 1 ; 1 ; 1 ), B ( − 4 ; 3 ; 1 ), C ( − 9 ; 5 ; 1 )
Bài 10. Cho ba điểm A, B, C.
Chứng tỏ ba điểm A, B, C tạo thành một tam giác .
Tìm toạ độ trọng tâm G của ∆ ABC.
Xác định điểm D sao cho ABCD là hình bình hành .
a. A ( 1 ; 2 ; − 3 ), B ( 0 ; 3 ; 7 ), C ( 12 ; 5 ; 0 )
b. A ( 0 ; 13 ; 21 ), B ( 11 ; − 23 ; 17 ), C ( 1 ; 0 ; 19 )
c. A ( 3 ; − 4 ; 7 ), B ( − 5 ; 3 ; − 2 ), C ( 1 ; 2 ; − 3 )
d. A ( 4 ; 2 ; 3 ), B ( − 2 ; 1 ; − 1 ), C ( 3 ; 8 ; 7 )
Bài 11. Trên trục Oy ( Ox ), tìm điểm cách đều hai điểm :
a ) A ( 3 ; 1 ; 0 ), B ( – 2 ; 4 ; 1 )
b ) A ( 1 ; – 2 ; 1 ), B ( 11 ; 0 ; 7 )
c ) A ( 4 ; 1 ; 4 ), B ( 0 ; 7 ; − 4 )
Bài 12. Trên mặt phẳng Oxy ( Oxz, Oyz ), tìm điểm cách đều ba điểm :
a. A ( 1 ; 1 ; 1 ), B ( − 1 ; 1 ; 0 ), C ( 3 ; 1 ; − 1 )
b. A ( − 3 ; 2 ; 4 ), B ( 0 ; 0 ; 7 ), C ( − 5 ; 3 ; 3 )
Bài 13. Cho hai điểm A, B. Đường thẳng AB cắt mặt phẳng Oyz ( Oxz, Oxy ) tại điểm M.
Điểm M chia đoạn thẳng AB theo tỉ số nào ?
Tìm tọa độ điểm M.
a ) A ( 2 ; − 1 ; 7 ), B ( 4 ; 5 ; − 2 )
b ) A ( 4 ; 3 ; − 2 ), B ( 2 ; − 1 ; 1 )
c. A ( 10 ; 9 ; 12 ), B ( − 20 ; 3 ; 4 )
Bài 14. Cho bốn điểm A, B, C, D.
Chứng minh A, B, C, D là bốn đỉnh của một tứ diện .
Tìm tọa độ trọng tâm G của tứ diện ABCD.
Tính góc tạo bởi những cạnh đối lập của tứ diện ABCD.

Tính thể tích của khối tứ diện ABCD.

Tính diện tích quy hoạnh tam giác BCD, từ đó suy ra độ dài đường cao của tứ diện vẽ từ A .

Xem thêm

Source: https://vh2.com.vn
Category : Trái Đất