Chuyên đề 8: Hình học không gian

Tailieumoi. vn xin ra mắt đến những quý thầy cô, những em học viên đang trong quy trình ôn tập tài liệu Chuyên đề 8 : Hình học không gian, tài liệu gồm có 36 trang. Tài liệu được tổng hợp từ những tài liệu ôn thi hay nhất giúp những em học viên có thêm tài liệu tìm hiểu thêm trong quy trình ôn tập, củng cố kỹ năng và kiến thức và sẵn sàng chuẩn bị cho kỳ thi sắp hới. Chúc những em học viên ôn tập thật hiệu suất cao và đạt được hiệu quả như mong đợi .
Mời những quý thầy cô và những em học viên cùng tìm hiểu thêm và tải về cụ thể tài liệu dưới đây

Chuyên đề 8: Hình học không gian

Hình học không gian

Các yếu tố trong tam giác cần nắm vững

+ Với tam giác ABC vuông tại A có đường cao AH khi đó
\ ( \ begin { array } { l } B { C ^ 2 } = A { B ^ 2 } + A { C ^ 2 } ; A { B ^ 2 } = BH \ cdot BC ; \ \ A { C ^ 2 } = CH.BC ; \ frac { 1 } { { A { H ^ 2 } } } = \ frac { 1 } { { A { B ^ 2 } } } + \ frac { 1 } { { A { C ^ 2 } } } \ end { array } \ )
+ Với tam giác ABC có những cạnh là a, b, c độ dài những trung tuyến \ ( { m_a }, { m_b }, { m_c } \ ) và có nửa đường kính đường tròn ngoại tiếp R, nửa đường kính đường tròn nội tiếp r, nửa chu vi là p khi đó
Định lý
\ ( \ begin { array } { l } { \ mathop { \ rm cosin } \ nolimits } : \ cos A = \ frac { { { b ^ 2 } + { c ^ 2 } – { a ^ 2 } } } { { 2 bc } }, \ \ \ cos B = \ frac { { { c ^ 2 } + { a ^ 2 } – { b ^ 2 } } } { { 2 ca } }, \ cos C = \ frac { { { a ^ 2 } + { b ^ 2 } – { c ^ 2 } } } { { 2 ab } } \ end { array } \ ) .
Từ đó tính được : \ ( \ sin A = \ sqrt { 1 – { { \ cos } ^ 2 } A }, \ sin B, \ sin C \ ) .
Định lý hàm số sin : \ ( \ frac { a } { { \ sin A } } = \ frac { b } { { \ sin B } } = \ frac { c } { { \ sin C } } = 2R \ )
Độ dài đường trung tuyến :
\ ( m_a ^ 2 = \ frac { { 2 \ left ( { { b ^ 2 } + { c ^ 2 } } \ right ) – { a ^ 2 } } } { 4 } ; m_b ^ 2 = \ frac { { 2 \ left ( { { c ^ 2 } + { a ^ 2 } } \ right ) – { b ^ 2 } } } { 4 } ; m_c ^ 2 = \ frac { { 2 \ left ( { { a ^ 2 } + { b ^ 2 } } \ right ) – { c ^ 2 } } } { 4 }. \ )
Diện tích tam giác :
\ ( \ begin { array } { l } S = \ frac { 1 } { 2 } a \ cdot { h_a } = \ frac { 1 } { 2 } b \ cdot { h_b } = \ frac { 1 } { 2 } c \ cdot { h_c } \ \ S = \ frac { 1 } { 2 } ab \ sin C = \ frac { 1 } { 2 } bc \ sin A = \ frac { 1 } { 2 } ca \ sin B \ \ S = \ frac { { abc } } { { 4R } } = pr = \ sqrt { p ( p – a ) ( p – b ) ( p – c ) } \ end { array } \ )
Với tam giác đều cạnh a thì có diện tích quy hoạnh là \ ( S = \ frac { { { a ^ 2 } \ sqrt 3 } } { 4 } \ )
Diện tích hình thang \ ( S = \ frac { 1 } { 2 } ( a + b ) \ cdot h ( a, b \ ) là hai cạnh đáy và h là độ cao )
Tứ giác có hai đường chéo vuông góc với nhau \ ( { S_ { ABCD } } = \ frac { 1 } { 2 } AC.BD \ )

Các công thức tính thể tích

+ V ( khối hộp chữ nhật ) = abc ( với a, b, c là ba size của hình hộp chữ nhật ) .
+ V ( khối chóp \ ( ) = \ frac { 1 } { 3 } dt \ ) ( đáy ). Chiều cao
+ V khối lăng trụ ) = dt ( đáy ). Chiều cao
+ V ( khối cầu \ ( ) = \ frac { 4 } { 3 } \ pi { R ^ 3 } \ )

Phương pháp xác định chiều cao của khối chóp

Loại 1: Khối chóp có một cạnh vuông góc với đáy đó chính là chiều cao của khối chóp.

Loại 2: Khối chóp có một mặt bên vuông góc với đáy thì đường cao chính là đường kẻ từ đỉnh khối chóp đến giao tuyến của mặt bên đó với đáy khối chóp.

Loại 3: Khối chóp có hai mặt bên kề nhau cùng vuông góc với đáy thì đường cao chính là giao tuyến của hai mặt bên đó.

Loại 4: Khối chóp có các cạnh bên bằng nhau hoặc cùng tạo với đáy một góc bằng nhau thì đường cao là đường kẻ từ đỉnh khối chóp đến tâm vòng tròn ngoại tiếp đáy.

Loại 5: Khối chóp có các mặt bên cùng tạo với đáy một góc bằng nhau thì đường cao là đường kẻ từ đỉnh đến tâm vòng tròn nội tiếp đáy.

Loại 6: Khối chóp có hai mặt bên cùng tạo với đáy một góc bằng nhau thì chân đường cao khối chóp hạ từ đỉnh sẽ nằm trên đường phân giác của góc tạo bởi hai cạnh nằm trên mặt đáy của hai mặt bên. Chẳng hạn khối chóp S.ABCD có hai mặt bên (SAC) và (SAB) cùng tạo với đáy góc \(\alpha \) khi đó chân đường cao của khối chóp hạ từ đỉnh S nằm trên đường phân giác của góc BAC.

Loại 7: Khối chóp có hai cạnh bên bằng nhau hoặc cùng tạo với đáy một góc bằng nhau thì chân đường cao hạ từ đỉnh khối chóp nằm trên đường trung trực nối giữa hai giao điểm của hai cạnh bên với đáy. Chẳng hạn khối chóp S.ABCD có cạnh SB = SD khi đó chân đường cao của khối chóp hạ từ đỉnh S nằm trên đường trung trực của BD.

Việc xác định chân đường cao của khối chóp giúp ta giải quyết bài toán

+ Tính thể tích khối chóp trải qua công thức V ( khối chóp ) \ ( = \ frac { 1 } { 3 } dt \ ) ( đáy ). chiều cao .

+ Tính góc tạo bởi đường thẳng hoặc mặt phẳng bên với đáy hoặc tính góc giữa hai mặt bên khối chóp (góc tạo bởi cạnh bên và mặt đáy chính là góc tạo bởi cạnh bên và đường thẳng nối chân đường cao khối chóp và giao điểm của cạnh bên với đáy). Chẳng hạn khối chóp S.ABCD có chân đường cao hạ từ đỉnh S của khối chóp là H khi đó góc tạo bởi cạnh bên SA và mặt phẳng đáy chính là góc giữa hai đường thẳng SA và AH.

+ Tính khoảng cách từ 1 điểm tói 1 mặt phẳng \ ( h = \ frac { { 3V } } { { { S_d } } } \ )

Phương pháp tính thể tích khối đa diện

+ Khi xác lập được chiều cao khối chóp thì vận dụng cách tính trực tiếp thể tích khối chóp nhờ công thức V ( khối chóp ) \ ( = \ frac { 1 } { 3 } dt \ ) ( đáy ). chiều cao .
+ Phân chia khối đa diện thành nhiều khối đa diện hơn và dễ tính thể tích hơn .
+ Dùng tỷ số thể tích .
Cho 3 đường thẳng không đồng thẳng SA, SB, SC những điểm \ [ A ‘ \ in SA ; B ‘ \ in SB ; C ‘ \ in SC \ ] khi đó ta có tỷ số thể tích .
\ ( \ begin { array } { l } \ frac { { V \ left ( { S { A ^ \ prime } { B ^ \ prime } { C ^ \ prime } } \ right ) } } { { V ( SABC ) } } = \ frac { { S { A ^ \ prime }. SB } } { { SA.SB } } \ \ \ frac { { V \ left ( { { A ^ \ prime } ABC } \ right ) } } { { V ( SABC ) } } = \ frac { { { A ^ \ prime } A } } { { SA } } \ end { array } \ )

Khoảng cách từ 1 điểm đến 1 mặt phẳng

– Nếu đường thẳng d song song với mặt phẳng ( P. ) thì khoảng cách từ mọi điểm trên d đến ( P. ) là như nhau .
– Đường thẳng d cắt mặt phẳng ( P. ) tại điểm M và có hai điểm A, B trên d sao cho AM = kBM thì d ( A ; ( P. ) ) = k. d ( B ; ( P. ) ). Áp dụng khi tính khoảng cách trực tiếp từ một điểm đến mặt phẳng khó khăn vất vả .

Tìm tâm và bán kính mặt cầu ngoại tiếp khối đa diện

Giả sử I là tâm mặt cầu ngoại tiếp khối đa diện \ ( S. { A_1 } { A_2 } \ ldots { A_n } \ ) khi đó
+ I thuộc trục đường tròn đáy là đường thẳng đi qua tâm đường tròn ngoại tiếp đáy và vuông góc với mặt phẳng đáy .
+ I cách đều toàn bộ những điểm \ ( S, { A_1 }, { A_2 }, \ ldots, { A_n } \ ) nên I phải nằm trên mặt phẳng trung trực của \ ( S { A_i } \ ) .
Để chứng tỏ những điểm đều thuộc một mặt cầu
+ Chứng minh những điểm cùng nhìn một cạnh dưới một góc \ ( { 90 ^ ^ \ circ } \ ) .
+ Chứng minh chúng cách đều một điểm nào đó .
Dưới đây trình diễn 4 bài toán cơ bản nhất, những em nên nắm vững để vận dụng vào bài thi
Bài toán cơ bản 1 : Cho khối chóp có diện tích quy hoạnh đáy là S và chiều cao khối chóp h khi đó thể tích khối chóp được xác lập theo công thức \ ( V = \ frac { 1 } { 3 } S.h \ ) .
Bài toán cơ bản 2 : Cho khối chóp S.ABC trên những cạnh SA ; SB ; SC lần lượt lấy những điểm A ’, B ’, C ’. Khi đó ta có :
\ ( \ frac { { { V_ { S.ABC } } } } { { { V_ { S. { A_1 } { B_1 } { C_1 } } } } } = \ frac { { SA } } { { S { A_1 } } } \ cdot \ frac { { SB } } { { S { B_1 } } } \ cdot \ frac { { SC } } { { S { C_1 } } } \ )
Bài toán cơ bản 3 : Cho tứ diện ABCD, có d là khoảng cách giữa hai đường thẳng AB, CD và \ ( \ alpha \ ) là góc giữa hai đường thẳng đó. Khi đó thể tích tứ diện ABCD được xác lập theo công thức \ ( { V_ { ABCD } } = \ frac { 1 } { 6 } AB \ cdot CD \ cdot d \ cdot \ sin \ alpha \ )
Chứng minh :

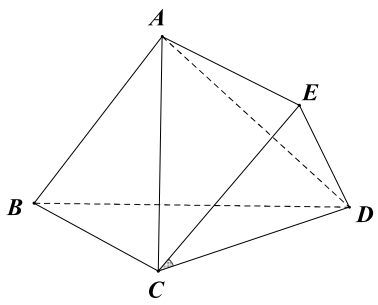
Dựng hình bình hành ABCE, khi đó \ ( \ widehat { ECD } = \ alpha \ )
Ta có \ ( { V_ { ABCD } } = { V_ { E.BCD } } = { V_ { B.CED } } ( \ ) do AE song song với mặt phẳng BCD )
Do AB song song với mặt phẳng CED nên khoảng cách giữa AB ; D cũng chính là khoảng cách từ B đến mặt phẳng CED
Vậy \ ( { V_ { ABCD } } = { V_ { B \ cdot CED } } \ )
\ ( \ begin { array } { l } = \ frac { 1 } { 3 } d ( B ; ( CED ) ) \ cdot \ frac { 1 } { 2 } CE \ cdot CD \ cdot \ sin \ alpha \ \ = \ frac { 1 } { 6 } AB \ cdot CD \ cdot d \ cdot \ sin \ alpha \ end { array } \ )
Bài toán cơ bản 4 : Tính thể tích khối tứ diện ABCD có những cặp đối bằng nhau

AB = CD = a ; AC = BD = b ; AD = BC  =c .

Lời giải
Dựng tứ diện APQR sao cho B ; C ; D lần lượt là trung điểm của QR ; RP ; PQ .

Xem thêm

Source: https://vh2.com.vn
Category : Trái Đất