Lý thuyết, bài tập về Hệ tọa độ trong không gian có đáp án

Tailieumoi. vn xin ra mắt đến các quý thầy cô, các em học viên đang trong quy trình ôn tập tài liệu bài tập Hệ tọa độ trong không gian Toán lớp 12, tài liệu gồm có 54 trang, tuyển chọn 114 bài tập Hệ tọa độ trong không gian không thiếu triết lý, chiêu thức giải cụ thể và giải thuật, giúp các em học viên có thêm tài liệu tìm hiểu thêm trong quy trình ôn tập, củng cố kiến thức và kỹ năng và chuẩn bị sẵn sàng cho kì thi tốt nghiệp trung học phổ thông môn Toán sắp tới. Chúc các em học viên ôn tập thật hiệu suất cao và đạt được tác dụng như mong đợi .
Tài liệu Lý thuyết, bài tập về Hệ tọa độ trong không gian có đáp án gồm các nội dung sau :

A. Tóm tắt lý thuyết

– Tóm tắt ngắn gọn kiến thức trọng tâm cần nhớ về Hệ tọa độ trong không gian

B. Phương pháp giải toán

Vấn đề 1. Xác định tọa độ điểm, tọa độ vectơ

– Tóm tắt ngắn gọn giải pháp giải và 2 ví dụ minh họa có giải thuật cụ thể

Vấn đề 2. Phương trình mặt cầu

– Tóm tắt ngắn gọn giải pháp giải và 2 ví dụ minh họa có giải thuật chi tiết cụ thể

Vấn đề 3. Viết phương trình mặt cầu

– Tóm tắt ngắn gọn giải pháp giải và 7 ví dụ minh họa có giải thuật cụ thể

Bài tập tự luyện

– Gồm 9 bài tập tự luận có giải thuật cụ thể giúp học viên rèn luyện

Bài tập trắc nghiệm 

– Gồm 114 câu hỏi trắc nghiệm có đáp án và giải thuật cụ thể giúp học viên rèn luyện
Mời các quý thầy cô và các em học viên cùng tìm hiểu thêm và tải về chi tiết cụ thể tài liệu dưới đây :

HỆ TỌA ĐỘ TRONG KHÔNG GIAN

A.TÓM TẮT LÝ THUYẾT

1. Tọa độ của vectơ

a) Định nghĩa: u→=x;y;z⇔u→=xi→+yj→+zk→ với i→,j→,k→ là các vectơ đơn vị, tương ứng trên các trục Ox Oy Oz

b) Tính chất: Cho hai vectơ a→=(a1;a2;a3) , b→=b1;b2;b3 và k là số thực tùy ý, ta có: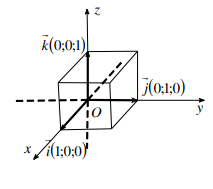

+ a → + b → = a1 + b1 ; a2 + b2 ; a3 + b3
+ a → – b → = a1-b1 ; a2-b2 ; a3-b3
+ ka → = ka1 ; ka2 ; ka3
+ a → = b → ⇔ a1 = b1a2 = b2a3 = b3
+ a → cùng phương b → ( b → khác 0 ) ⇔ a1 = kb1a2 = kb2a3 = kb3 ⇔ a1b1 = a2b2 = a3b3
+ a →. b → = a1. b1 + a2. b2 + a3. b3
+ a → ⊥ b → ⇔ a →. b → = 0 ⇔ a1. b1 + a2. b2 + a3. b3 = 0
+ a → 2 = a12 + a22 + a32 suy ra a → = a → 2 = a12 + a22 + a32
+ cos ( a → ; b → ) = a. → b → a. → b → = a1b1 + a2b2 + a3b3a12 + a22 + a32b12 + b22 + b32

2. Tọa độ của điểm

a) Định nghĩa: M(x;y;z)⇔OM→=x;y;z ( x : hoành độ, y tung độ, z cao độ).

Chú ý: Trong hệ tọa độ Oxyz, cho điểm M(x;y;z) ta có các khẳng định sau:

• M≡O⇔M(0;0;0)

• M ∈ Oxy ⇔ z = 0, tức là M ( x ; y ; 0 )
• M ∈ Oyz ⇔ x = 0, tức là M ( 0 ; y ; z )
• M ∈ Oxz ⇔ y = 0, tức là M ( x ; 0 ; z )
Xem thêm

Source: https://vh2.com.vn
Category : Trái Đất