Đồ họa của Tech Insider cho thấy những lục địa sẽ hợp nhất thành một dải đất duy nhất trong vòng 250 triệu năm tới . Bạn đang đọc: Các...
Tọa độ trọng tâm tam giác: Lý thuyết, Cách tìm và Các dạng bài tập
Trọng tâm tam giác là một điểm quan trọng và có nhiều ứng dụng trong các bài toán. Vậy trọng tâm tam giác là gì? Tọa độ trọng tâm tam giác? Các công thức trọng tâm tam giác?…. Trong nội dung bài viết dưới đây, DINHNGHIA.VN sẽ giúp bạn tổng hợp kiến thức về chủ đề này nhé!
Trọng tâm tam giác là gì?
Cho tam giác \( ABC \). Ba đường trung tuyến xuất phát từ ba đỉnh của tam giác đồng quy tại một điểm \( G \).Điểm \( G \) đó được gọi là trọng tâm của tam giác \( ABC \)
Tính chất trọng tâm của tam giác
Khoảng cách từ trọng tâm tới mỗi đỉnh bằng \(\frac{2}{3}\) độ dài đường trung tuyến tương ứng với đỉnh đó.
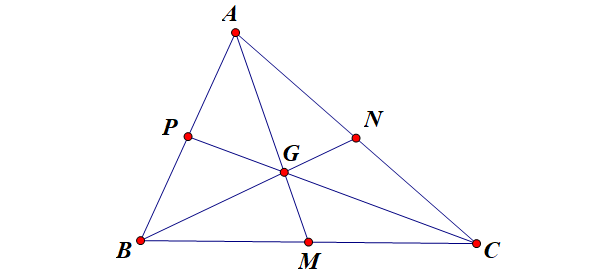
\ ( \ frac { AG } { AM } = \ frac { BG } { BN } = \ frac { CG } { CP } = \ frac { 2 } { 3 } \ )
\ ( \ overrightarrow { GA } + \ overrightarrow { GB } + \ overrightarrow { GC } = 0 \ )
Cách tìm tọa độ trọng tâm tam giác
Tọa độ trọng tâm tam giác trong mặt phẳng
Trong mặt phẳng \ ( Oxy \ ) cho tam giác \ ( ABC \ ) có tọa độ ba đỉnh lần lượt là : \ ( A ( x_A ; y_A ) ; B ( x_B ; y_B ) ; C ( x_C ; y_C ) \ ). Khi đó tọa độ trọng tâm \ ( G \ ) của tam giác \ ( ABC \ ) là : \ ( G ( \ frac { x_A + x_B + x_C } { 3 } ; \ frac { y_A + y_B + y_C } { 3 } ) \ )
Chứng minh:
Gọi \ ( AM ; BN ; CP \ ) lần lượt là ba đường trung tuyến của tam giác \ ( ABC \ )
Vì \( M \) là trung điểm \( BC \) nên \(\Rightarrow M(\frac{x_B+x_C}{2};\frac{y_B+y_C}{2}) \;\;\;\;\; (1) \)
Do \ ( \ frac { AG } { AM } = \ frac { 2 } { 3 } \ Rightarrow \ frac { GA } { GM } = 2 \ )
\ ( \ Rightarrow G ( \ frac { x_A + 2 x_M } { 3 } ; \ frac { y_A + 2 y_M } { 3 } ) \ ; \ ; \ ; \ ; \ ; ( 2 ) \ )
Thay \ ( ( 1 ) \ ) vào \ ( ( 2 ) \ ) ta được
\ ( G ( \ frac { x_A + x_B + x_C } { 3 } ; \ frac { y_A + y_B + y_C } { 3 } ) \ )
Ví dụ:
Trong mặt phẳng \ ( Oxy \ ) cho tam giác \ ( ABC \ ) vuông tại \ ( A \ ) có \ ( AB = AC \ ). Biết rằng \ ( M ( 1 ; – 1 ) \ ) là trung điểm \ ( BC \ ) và \ ( \ Rightarrow G ( \ frac { 2 } { 3 } ; 0 ) \ ) là trọng tâm của \ ( \ Delta ABC \ ). Tìm tọa độ những đỉnh của \ ( \ Delta ABC \ )
Cách giải:

Vì \ ( G \ ) là trọng tâm tam giác \ ( ABC \ ) nên :
\ ( \ Rightarrow G ( \ frac { x_A + 2 x_M } { 3 } ; \ frac { y_A + 2 y_M } { 3 } ) \ )
\ ( \ Rightarrow A ( 3 x_G – 2 x_M ; 3 y_G – 2 y_M ) \ Rightarrow A ( 0 ; 2 ) \ )
\ ( \ Rightarrow \ overrightarrow { AM } = ( – 1 ; 3 ) \ )
Vì \ ( \ Delta ABC \ ) vuông cân tại \ ( A \ ) có \ ( AM \ ) là trung tuyến \ ( \ Rightarrow AM \ bot BC \ )
\ ( \ Rightarrow \ overrightarrow { AM } \ ) là véc tơ pháp tuyến của \ ( BC \ )
\ ( \ Rightarrow \ ) phương trình \ ( BC : – 1 ( x-1 ) + 3 ( y + 1 ) = 0 \ )
\ ( \ Rightarrow BC : – x + 3 y + 4 = 0 \ )
Vì \ ( \ Delta ABC \ ) vuông nên \ ( \ Rightarrow AM = \ frac { BC } { 2 } = BM = CM \ )
\ ( B ( 3 a + 4 ; a ) \ Rightarrow BM ^ 2 = ( 3 a + 3 ) ^ 2 + ( a + 1 ) ^ 2 = 10 ( a + 1 ) ^ 2 \ )
\ ( AM ^ 2 = 1 ^ 2 + 3 ^ 2 = 10 \ )
\ ( \ Rightarrow 10 = 10 ( a + 1 ) ^ 2 \ Rightarrow ( a + 1 ) ^ 2 = 1 \ Rightarrow \ left [ \ begin { array } { l } a = 0 \ \ a = – 2 \ end { array } \ right. \ )
Vậy \ ( \ left [ \ begin { array } { l } B ( 4 ; 0 ) \ Rightarrow C ( – 2 ; – 2 ) \ \ B ( – 2 ; – 2 ) \ Rightarrow C ( 4 ; 0 ) \ end { array } \ right. \ )
Vậy tọa độ ba đỉnh \ ( \ Delta ABC \ ) là \ ( A ( 0 ; 2 ) ; B ( 4 ; 0 ) ; C ( – 2 ; – 2 ) \ ) hoặc \ ( A ( 0 ; 2 ) ; B ( – 2 ; – 2 ) ; C ( 4 ; 0 ) \ )
Tọa độ trọng tâm tam giác trong không gian
Trong không gian \ ( Oxyz \ ) cho tam giác \ ( ABC \ ) có tọa độ ba đỉnh lần lượt là : \ ( A ( x_A ; y_A ; z_A ) ; B ( x_B ; y_B ; z_B ) ; C ( x_C ; y_C ; z_C ) \ ). Khi đó tọa độ trọng tâm \ ( G \ ) của tam giác \ ( ABC \ ) là : \ ( G ( \ frac { x_A + x_B + x_C } { 3 } ; \ frac { y_A + y_B + y_C } { 3 } ; \ frac { z_A + z_B + z_C } { 3 } ) \ )
Chứng minh:
Tương tự phần chứng tỏ trong mặt phẳng
Ví dụ:
Trong không gian \ ( Oxyz \ ) cho tam giác \ ( ABC \ ) có tọa độ \ ( B ( 1 ; 1 ; 0 ) ; C ( 3 ; – 1 ; 2 ) \ ) và trọng tâm \ ( G ( 2 ; 0 ; 0 ) \ ). Viết phương trình đường cao \ ( AH \ ) của tam giác \ ( ABC \ )
Cách giải:

Ta có :
\ ( A ( 3 x_G – x_B-x_C ; 3 y_G – y_B-y_C ; 3 z_G – z_B-z_C ) \ )
\ ( \ Rightarrow A ( 2 ; 0 ; – 2 ) \ )
\ ( \ overrightarrow { BC } = ( 2 ; – 2 ; 2 ) \ Rightarrow \ ) phương trình \ ( BC \ ) :
\(\left\{\begin{matrix} x=1+t\\y=1-t \\ z=t \end{matrix}\right.\)
Giả sử \ ( H ( 1 + a ; 1 – a ; a ) \ )
\ ( \ Rightarrow \ overrightarrow { AH } = ( a-1 ; 1 – a ; a + 2 ) \ )
Vì \ ( AH \ bot BC \ Rightarrow ( a-1 ) + ( a-1 ) + ( a + 2 ) = 0 \ Rightarrow a = 0 \ )
\ ( \ Rightarrow H \ equiv B \ )
\ ( \ overrightarrow { AB } = ( – 1 ; 1 ; 2 ) \ Rightarrow \ ) phương trình đường cao :
\ ( \ left \ { \ begin { matrix } x = 1 – t \ \ y = 1 + t \ \ z = 2 t \ end { matrix } \ right. \ )
Các công thức trọng tâm tam giác
Sau đây là một số ít công thức trọng tâm tam giác giúp xử lý nhanh những câu hỏi trắc nghiệm .

Cho tam giác \ ( ABC \ ) có \ ( AM ; BN ; CP \ ) là ba đường trung tuyến, cắt nhau tại \ ( G \ ) là trọng tâm của tam giác. Khi đó ta có :
- Diện tích các tam giác nhỏ bằng nhau:
\ ( S _ { APG } = S_ { ANG } = S_ { CNG } = S_ { CMG } = S_ { BMG } = S_ { BPG } = \ frac { S_ { ABC } } { 6 } \ )
\ ( S _ { ABG } = S_ { ACG } = S_ { BCG } = \ frac { S_ { ABC } } { 3 } \ )
- Độ dài các đường trung tuyến:
\ ( AM = \ frac { \ sqrt { 2AB ^ 2 + 2AC ^ 2 – BC ^ 2 } } { 2 } \ )
\ ( BN = \ frac { \ sqrt { 2BA ^ 2 + 2BC ^ 2 – AC ^ 2 } } { 2 } \ )
\ ( CP = \ frac { \ sqrt { 2CA ^ 2 + 2CB ^ 2 – AB ^ 2 } } { 2 } \ )
\ ( \ Rightarrow AM ^ 2 + BN ^ 2 + CP ^ 2 = \ frac { 3 } { 4 } ( AB ^ 2 + BC ^ 2 + CA ^ 2 ) \ )
- Gọi \( H \) là chân đường cao hạ từ đỉnh \( A \) xuống \( BC \). Khi đó :
\ ( | AB ^ 2 – AC ^ 2 | = 2BC. MH \ )
Ví dụ:
Cho tam giác \ ( ABC \ ) có độ dài ba cạnh lần lượt là \ ( AB = 4 cm ; AC = 7 cm ; BC = 8 cm \ ). Gọi \ ( G \ ) là trọng tâm tam giác \ ( ABC \ ). Tính độ dài đoạn \ ( AG \ )
Cách giải:
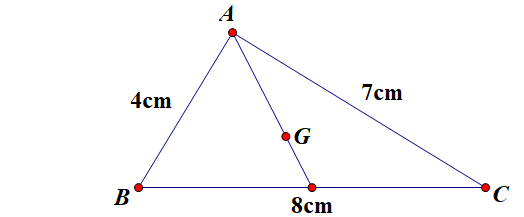
Áp dụng công thức độ dài đường trung tuyến, ta có :
\ ( AG = \ frac { 2 } { 3 }. \ frac { \ sqrt { 2AB ^ 2 + 2AC ^ 2 – BC ^ 2 } } { 2 } = \ frac { 2 } { 3 }. \ frac { \ sqrt { 66 } } { 2 } = \ frac { \ sqrt { 66 } } { 3 } \ )
Bài viết trên đây của DINHNGHIA.VN đã giúp bạn tổng hợp các công thức và bài toán về tọa độ trọng tâm trong tam giác. Hy vọng những kiến thức trong bài viết sẽ giúp ích cho bạn trong quá trình học tập và nghiên cứu chủ đề tọa độ trọng tâm tam giác. Chúc bạn luôn học tốt!.
Xem thêm:
2.3
/
5
(
3
bầu chọn
)
Xem thêm: Những bức ảnh về ‘Trái đất xưa và nay’: Trái đất đã thay đổi như thế nào trong hơn 100 năm qua?
Please follow and like us :
![]()
![]()
Source: https://vh2.com.vn
Category : Trái Đất





