Đề 3 trang 135 SBT Hình học 12: Trong không gian Oxyz cho bốn điểm A(2; 4; -1),B(1; 4; -1),C(2; 4; 3),…

ĐỀ 3 (45 PHÚT)

Trang 135 sách bài tập (SBT) – Hình học 12

Trong không gian Oxyz cho bốn điểm A(2; 4; -1),B(1; 4; -1),C(2; 4; 3), D(2; 2; -1).

a ) ( 2 điểm ) Chứng minh rằng những đường thẳng AB, AC, AD vuông góc với nhau từng đôi một .
b ) ( 2 điểm ) Viết phương trình tham số của đường vuông góc chung \ ( \ Delta \ ) của hai đường thẳng AB và CD .
c ) ( 3 điểm ) Viết phương trình mặt cầu ( S ) đi qua bốn điểm A, B, C, D .
d ) ( 3 điểm ) Viết phương trình mặt phẳng \ ( ( \ alpha ) \ ) tiếp xúc với mặt cầu ( S ) và song song với mặt phẳng ( ABD ) .

Hướng dẫn làm bài

a ) Ta có \ ( \ overrightarrow { AB } = ( – 1 ; 0 ; 0 ) ; \ overrightarrow { AC } = ( 0 ; 0 ; 4 ) ; \ overrightarrow { AD } = ( 0 ; – 2 ; 0 ) \ )
\ ( \ overrightarrow { AB }. \ overrightarrow { AC } = \ overrightarrow { AC }. \ overrightarrow { AD } = \ overrightarrow { AD }. \ overrightarrow { AB } = 0 \ ), suy ra \ ( AB \ bot AC, AC \ bot AD, AD \ bot AB \ )
Vậy AB, AC, AD vuông góc với nhau từng đôi một .
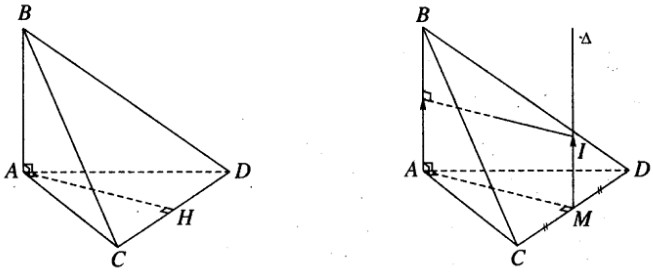
b ) Gọi H là hình chiếu vuông góc của A trên CD. Ta có AH chính là đường vuông góc chung của AB và CD ( hình 3.34 )

Quảng cáo – Advertisements

\ ( \ overrightarrow { AB } = ( – 1 ; 0 ; 0 ) ; \ overrightarrow { CD } = ( 0 ; – 2 ; – 4 ) \ )
Vecto chỉ phương của đường thẳng AH là \ ( \ overrightarrow a = \ overrightarrow { AB } \ wedge \ overrightarrow { CD } = ( 0 ; – 4 ; 2 ) \ ) .
Phương trình tham số của đường thẳng AH hay \ ( \ Delta \ ) là \ ( \ left \ { { \ matrix { { x = 2 } \ cr { y = 4 – 4 t } \ cr { z = – 1 + 2 t } \ cr } } \ right. \ )
c ) Gọi M trung điểm của CD. Vẽ trục \ ( \ Delta \ ) của đường tròn ( ACD ), mặt phẳng trung trực của AB cắt \ ( \ Delta \ ) tại I ( a ; b ; c ). Ta có I là tâm của mặt cầu ( S ) ngoại tiếp tứ diện ABCD ( h. 3.35 )
Ta có M ( 2 ; 3 ; 1 ), \ ( \ overrightarrow { MI } = { 1 \ over 2 } \ overrightarrow { AB } \ Rightarrow \ left \ { { \ matrix { { a – 2 = – { 1 \ over 2 } } \ cr { b – 3 = 0 } \ cr { c – 1 = 0 } \ cr } } \ right. \ Rightarrow \ left \ { { \ matrix { { a = { 3 \ over 2 } } \ cr { b = 3 } \ cr { c = 1 } \ cr } } \ right. \ )
( S ) có nửa đường kính \ ( r = IA = \ sqrt { { 1 \ over 4 } + 1 + 4 } = { { \ sqrt { 21 } } \ over 2 } \ )
Vậy phương trình mặt cầu ( S ) ngoại tiếp tứ diện ABCD là :
\ ( { ( x – { 3 \ over 2 } ) ^ 2 } + { ( y – 3 ) ^ 2 } + { ( z – 1 ) ^ 2 } = { { 21 } \ over 4 } \ )

d) Mặt phẳng \((\alpha )\) song song với (ABD) nên có vecto pháp tuyến là \(\overrightarrow {AC}  = (0;0;4)\)  hay \(\overrightarrow n  = (0;0;1)\)

Phương trình \ ( ( \ alpha ) \ ) có dạng z + D = 0. Ta có :
\ ( ( \ alpha ) \ ) tiếp xúc với S ( I, r ) \ ( \ Leftrightarrow d ( I, ( \ alpha ) ) = r \ Leftrightarrow | 1 + D | = { { \ sqrt { 21 } } \ over 2 } \ Leftrightarrow \ left [ { \ matrix { { D = { { \ sqrt { 21 } } \ over 2 } – 1 } \ cr { D = – { { \ sqrt { 21 } } \ over 2 } – 1 } \ cr } } \ right. \ )
Vậy có hai mặt phẳng \ ( ( \ alpha ) \ ) thỏa mãn nhu cầu đề bài là : \ ( ( { \ alpha _1 } ) : z + { { \ sqrt { 21 } } \ over 2 } – 1 = 0 \ ) và \ ( ( { \ alpha _2 } ) : z – { { \ sqrt { 21 } } \ over 2 } – 1 = 0 \ )

Source: https://vh2.com.vn
Category : Trái Đất