Lý thuyết và các dạng bài tập quang phổ vạch của nguyên tử Hyđrô ( đầy đủ)

Bài viết trình bày tóm tắt lý thuyết về sự dịch chuyển các vạch quang phổ của nguyên tử Hiđrô và các bài tập liên quan như tìm bước sóng, năng lượng, số vạch bức xạ…

LÝ THUYẾT VÀ CÁC DẠNG BÀI TẬP QUANG PHỔ VẠCH CỦA NGUYÊN TỬ HYĐRÔ

1. Tóm tắt lý thuyết và công thức: 

Bạn đang đọc: Lý thuyết và các dạng bài tập quang phổ vạch của nguyên tử Hyđrô ( đầy đủ)

Tiên đề Bo : \(e=hf_{nm}=\frac{hc}{l_{_{_{nm}}}}=E_{n}-E_{m}\)

+ Bán kính quỹ đạo dừng thứ n của electron trong nguyên tử hiđrô :

                     rn = n2r0   Với r0 =5,3.10-11m là bán kính Bo (ở quỹ đạo K)

+ Khi nguyên tử đang ở mức nguồn năng lượng cao chuyển xuống mức nguồn năng lượng thấp thì phát ra photon, ngược lại chuyển từ mức nguồn năng lượng thấp chuyển lên mức nguồn năng lượng cao nguyên tử sẽ hấp thu photon\ ( E_ { cao } – E_ { thấp } = hf \ )

Lưu ý: Bước sóng dài nhất \(\lambda _{NM}\) khi e chuyển từ N \(\rightarrow\) M.

Bước sóng ngắn nhất \ ( \ lambda _ { \ infty M } \ ) khi e chuyển từ \ ( \ infty \ rightarrow \ ) M .+ Bước sóng phát ra khi nguyên tử chuyển mức nguồn năng lượng : \ ( \ varepsilon = E_ { n } – E_ { m } \ )\ ( hf_ { nm } = \ frac { hc } { l_ { nm } } = E_ { n } – E_ { m } \ Rightarrow \ frac { 1 } { \ lambda _ { nm } } = \ frac { E_ { N } – E_ { M } } { hc } \ ) \ ( \ Rightarrow \ lambda _ { nm } = \ frac { hc } { E_ { n } – E_ { m } } = \ frac { hc } { E_ { 0 } \ left ( \ frac { 1 } { n ^ { 2 } } – \ frac { 1 } { m ^ { ^ { 2 } } } \ right ) } \ )+ Tần số của phôtôn bức xạ \ ( f_ { nm } = \ frac { c } { \ lambda _ { nm } } = \ frac { E_ { n } – E_ { m } } { h } \ ) Với En > Em .+ Mối liên hệ giữa những bước sóng và tần số của những vạch quang phổ của nguyên từ hiđrô :\ ( \ frac { 1 } { \ lambda _ { 31 } } = \ frac { 1 } { \ lambda _ { 32 } } + \ frac { 1 } { \ lambda _ { 21 } } \ ) và \ ( f_ { 31 } = f_ { 32 } + f_ { 21 } \ ) ( như cộng véctơ )+ Công thức thực nghiệm : \ ( \ frac { 1 } { \ lambda } = R_ { H } \ left ( \ frac { 1 } { m ^ { 2 } } – \ frac { 1 } { n ^ { 2 } } \ right ) \ )+ Hằng số Rydberg : \ ( R_ { H } = \ frac { E_ { _ { 0 } } } { h. c } = \ frac { 13,6 e } { h. c } = 1,0969. 10 ^ { 7 } m = 1,097. 10 ^ { 7 } m \ ) ( trong máy tính Fx thì RH là \ ( R_ { \ infty } \ ) )

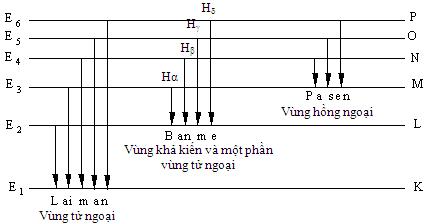
Các dãy Quang phổ của nguyên tử hidrô

– Dãy Laiman: khi e (n>1) về quĩ đạo K(m=1) thì phát ra các vạch thuộc dãy  Laiman: m= 1; n= 2,3,4…

\ ( \ frac { 1 } { \ lambda n1 } = \ frac { E_ { 0 } } { hc } \ left ( \ frac { 1 } { 1 ^ { 2 } } – \ frac { 1 } { n ^ { 2 } } \ right ) \ ) với \ ( n \ geq 2 \ ) Các vạch thuộc vùng tử ngoại

– Dãy Banme: Khi e chuyển từ quĩ đạo ngoài (n>2) về quĩ đạo L(m=2) thì phát ra các vạch thuộc dãy Banme: m= 2; n= 3,4,5…

\ ( \ frac { 1 } { \ lambda n2 } = \ frac { E_ { 0 } } { hc } \ left ( \ frac { 1 } { 2 ^ { 2 } } – \ frac { 1 } { n ^ { 2 } } \ right ) \ ) với \ ( n \ geq 3 \ ) Gồm 4 vạch : đỏ \ ( H_ { \ alpha } ( 0,656 \ mu m ) \ ), lam \ ( H_ { \ beta } ( 0,486 \ mu m ) \ ) ,chàm \ ( H_ { \ gamma } ( 0,434 \ mu m ) \ ), tím \ ( H_ { \ delta } ( 0,410 \ mu m ) \ ) và một phần ở vùng tử ngoại

– Dãy Pasen : khi các e chuyển từ quĩ đạo bên ngoài (n>3) về quĩ đạo M(m=3): m = 3; n = 4, 5, 6…

\ ( \ frac { 1 } { \ lambda n3 } = \ frac { E_ { 0 } } { hc } \ left ( \ frac { 1 } { 3 ^ { 2 } } – \ frac { 1 } { n ^ { 2 } } \ right ) \ ) với \ ( n \ geq 4 \ ) Các vạch thuộc vùng hồng ngoại

Năng lượng của êlectron trong nguyên tử Hiđrô có biểu thức: 

+ Năng lượng electron trong nguyên tử hiđrô : \ ( E_ { n } = \ frac { E_ { 0 } } { n ^ { 2 } } = – \ frac { 13,6 } { n ^ { 2 } } ( eV ) \ ) Với n \ ( \ in \ ) N * : lượng tử số .

E0 = – 13,6eV: năng lượng ở trạng thái cơ bản (Chú ý E0 < 0 )

– n = 1 ứng với quỹ đạo K ( nguồn năng lượng thấp nhất )- n = 2 ứng với quỹ đạo L. ..+ m = 1 ; n = 2, 3, 4 … dãy Laiman ( tử ngoại ) ;+ m = 2 ; n = 3, 4, 5 … dãy Banme ( một phần nhìn thấy )+ m = 3 ; n = 4, 5, 6 … dãy Pasen ( hồng ngoại ) .

 F Các bức xạ của dãy Banmer( nhìn thấy):

+ Vạch đỏ \ ( H_ { \ alpha } : \ lambda _ { \ alpha } = \ lambda _ { ML } = \ lambda _ { 32 } : \ frac { hc } { \ lambda _ { 32 } } = E_ { 3 } – E_ { 2 } \ )+ Vạch lam \ ( H_ { \ beta } : \ lambda _ { \ beta } = \ lambda _ { NL } = \ lambda _ { 42 } : \ frac { hc } { \ lambda _ { 4 } } = E_ { 4 } – E_ { 2 } \ )+ Vạch chàm \ ( H_ { \ gamma } : \ lambda _ { \ gamma } = \ lambda _ { OL } = \ lambda _ { 52 } : \ frac { hc } { \ lambda _ { 52 } } = E_ { 5 } – E_ { 2 } \ )+ Vạch tím \ ( H_ { \ theta } : \ lambda _ { \ theta } = \ lambda _ { PL } = \ lambda _ { 62 } : \ frac { hc } { \ lambda _ { 62 } } = E_ { 6 } – E_ { 2 } \ )

 Các vạch có bước sóng dài nhất của các dãy:

+ Dãy Laiman : \ ( \ lambda _ { 21 } : \ frac { hc } { \ lambda _ { 21 } } = E_ { 2 } – E_ { 1 } \ )+ Dãy Banmer : \ ( \ lambda _ { 32 } : \ frac { hc } { \ lambda _ { 32 } } = E_ { 3 } – E_ { 2 } \ )+ Dãy Paschen : \ ( \ lambda _ { 43 } : \ frac { hc } { \ lambda _ { 43 } } = E_ { 4 } – E_ { 3 } \ )

Chú ý: Khi nguyên tử ở trạng thái kích thích thứ n có thể (khả dĩ) phát ra số bức xạ điện từ cho bởi:

\ ( N = C_ { n } ^ { 2 } = \ frac { n ! } { ( n-2 ) ! 2 ! } \ ) trong đó \ ( C_ { n } ^ { 2 } \ ) là tổng hợp chập 2 của n .

2. Bài tập về các dãy quang phổ hidrô:

Ví dụ 1 về các bước sóng dãy Lymain (tử ngoại):

Khi electron trong nguyên tử hiđro ở một trong những mức năng lương cao L, M, N, O … nhảy về mức năng lương K, thì nguyên tử hiđro phát ra vạch bức xạ của dãy Lyman thuộc vùng tử ngoại của thang sóng điện từ, đơn cử như sau :+ Vạch tiên phong có bước sóng lớn nhất ứng với mức năng lương m = 1 \ ( \ rightarrow \ ) n = 2\ ( { { hc } \ over { { \ lambda _1 } } } = { E_2 } – { E_1 } = – { { 13,6 ( eV ) } \ over { { 2 ^ 2 } } } – \ left ( { – { { 13,5 ( eV ) } \ over { { 1 ^ 2 } } } } \ right ) = { { 3.13,6 } \ over 4 } ( eV ) \ )\ ( \ Rightarrow \ lambda _ { 21 } = \ frac { h. c. 4 } { 3.13,6. e } = 1,215. 10 ^ { – 7 } m = 0,1215 \ mu m \ )

Hoặc dùng công thức:  \(\frac{1}{\lambda }=R_{H}\left ( \frac{1}{m^{2}}-\frac{1}{n^{2}} \right )\) \(\rightarrow\) Thế số \(\lambda _{21}=\frac{1}{R_{H}\left ( \frac{1}{1^{2}}-\frac{1}{2^{2}} \right )}=1,215.10^{-7}m=0,1215\mu m\)

+Vạch thứ 2  ứng mức năng lương m = 1 \(\rightarrow\) n = 3, \(\lambda _{31}=\frac{1}{R_{H}\left ( \frac{1}{1^{2}}-\frac{1}{3^{2}} \right )}=1,025175.10^{-7}m=0,1025\mu m\)

+Vạch thứ 3 ứng mức năng lương m = 1 \(\rightarrow\) n = 4, \(\lambda _{41}=\frac{1}{R_{H}\left ( \frac{1}{1^{2}}-\frac{1}{2^{4}} \right )}=9,72018.10^{-8}m=0,0972\mu m\)

+ Vạch thứ 4 ứng  mức năng lương m = 1 \(\rightarrow\) n = 5, \(\lambda _{51}=\frac{1}{R_{H}\left ( \frac{1}{1^{2}}-\frac{1}{5^{2}} \right )}=9,492365.10^{-8}m=0,0949\mu m\)

+ Vạch thứ 5 ứng  mức năng lương m = 1 \(\rightarrow\) n = 6,\(\lambda _{61}=\frac{1}{R_{H}\left ( \frac{1}{1^{2}}-\frac{1}{6^{2}} \right )}=9,37303.10^{-8}m=0,09373\mu m\)

– – – – – – – – – – – – – – – – –  – –

+ Vạch ở đầu cuối có bước sóng nhỏ nhất ứng với mức nguồn năng lượng m = 1 \ ( \ rightarrow \ ) n = \ ( \ infty \ )

 \(\lambda _{\infty 1}=\frac{1}{R_{H}\left ( \frac{1}{1^{2}}-\frac{1}{\infty ^{2}} \right )}=\frac{1}{R_{H}}=,11267.10^{-8}m=0,0911\mu m\)                                                               

Ví dụ 2 về các bước sóng dãy Banme (có 4 vạch nhìn thấy: đỏ,  lam, chàm, tím)

Khi electron trong nguyên tử hiđro ở một trong các mức năng lương cao M, N, O,P… nhảy về mức năng lương L ( ứng với trường hợp nguyên tử từ mức cao hơn trở về mức 2), thì nguyên tử hiđro phát ra vạch bức xạ thuộc dãy Balmer ,bốn vạch đầu ở vùng nhìn thấy (đỏ, lam, chàm, tím) và một phần thuộc vùng tử ngoại của thang sóng điện từ, cụ thể như sau:

a.Dùng công thức :  \(E_{n}=\frac{E_{0}}{n^{2}}=-\frac{13,6}{n^{2}}(eV)\) với n =  2,3,4…

Các bức xạ thuộc dãy banme ứng với trường hợp nguyên tử từ mức cao hơn trở về mức 2+ Vạch thứ 1 có bước sóng lớn nhất màu đỏ ứng với mức năng lương n = 3 \ ( \ rightarrow \ ) m = 2, theo Anh xtanh :

                                       \(\frac{hc}{\lambda _{32}}=E_{3}-E_{2}\Rightarrow \lambda _{32}=\lambda _{\alpha }=0,656\mu m\)  (màu đỏ)

+ Vạch thứ 2 có màu lam ứng mức năng lương n = 4 \ ( \ rightarrow \ ) m = 2, có bước sóng được xác lập :

                                       \(\frac{hc}{\lambda _{42}}=E_{4}-E_{2}\Rightarrow \lambda _{42}=\lambda _{\beta }=0,486\mu m\)  (màu lam)

+ Vạch thứ 3 có màu chàm ứng mức năng lương n = 5 \ ( \ rightarrow \ ) m = 2, có bước sóng được xác lập :

                                      \(\frac{hc}{\lambda _{52}}=E_{5}-E_{2}\Rightarrow \lambda _{52}=\lambda _{\gamma }=0,434\mu m\)  (màu chàm)

+ Vạch thứ 4 có màu tím ứng mức năng lương n = 6 — > m = 2, có bước sóng được xác lập :

                                      \(\frac{hc}{\lambda _{62}}=E_{6}-E_{2}\Rightarrow \lambda _{62}=\lambda _{\delta }=0,410\mu m\)  (màu tím)

b.Hoặc dùng công thức : \(\frac{1}{\lambda }=R_{H}\left ( \frac{1}{2^{2}}-\frac{1}{n^{2}} \right )\Rightarrow \lambda = \frac{1}{R_{H}\left ( \frac{1}{2^{2}}-\frac{1}{n^{2}} \right )}\)  (dãy Balmer ứng với m =2).

+ Vạch thứ 1 có bước sóng lớn nhất màu đỏ ứng với mức năng lương n =3 \(\rightarrow\)  m = 2, được xác định \(\frac{1}{\lambda_{32} }=R_{H}\left ( \frac{1}{2^{2}}-\frac{1}{3^{2}} \right )\Rightarrow \lambda_{32} = \frac{1}{R_{H}\left ( \frac{1}{2^{2}}-\frac{1}{3^{2}} \right )}=6,5611.10^{-7}m=0,656\mu m\)\(=\lambda _{\alpha }\) (màu đỏ)

Xem thêm: Hướng dẫn kê khai thuế điện tử – Đại lý Thuế Việt An

+Vạch thứ 2 có màu lam ứng mức năng lương  n = 4 \(\rightarrow\) m = 2, có bước sóng được xác định: \(\frac{1}{\lambda_{42} }=R_{H}\left ( \frac{1}{2^{2}}-\frac{1}{4^{2}} \right )\Rightarrow \lambda_{42} = \frac{1}{R_{H}\left ( \frac{1}{2^{2}}-\frac{1}{4^{2}} \right )}=4,8600936.10^{-7}m\) \(=0.486\mu m=\lambda _{\beta }\) (màu lam )

+Vạch thứ 3 có màu chàm ứng mức năng lương n = 5 \(\rightarrow\) m = 2, có bước sóng được xác định:                  \(\frac{1}{\lambda_{52} }=R_{H}\left ( \frac{1}{2^{2}}-\frac{1}{5^{2}} \right )\Rightarrow \lambda_{52} = \frac{1}{R_{H}\left ( \frac{1}{2^{2}}-\frac{1}{5^{2}} \right )}=4,33936.10^{-7}m\)\(=0,434\mu m=\lambda _{\gamma }\) (màu chàm )

+Vạch thứ 4 có màu tím ứng mức năng lương n= 6 \(\rightarrow\) m = 2, có bước sóng được xác định: \(\frac{1}{\lambda_{62} }=R_{H}\left ( \frac{1}{2^{2}}-\frac{1}{6^{2}} \right )\Rightarrow \lambda_{62} = \frac{1}{R_{H}\left ( \frac{1}{2^{2}}-\frac{1}{6^{2}} \right )}=4,1007.10^{-7}m=0,410\mu m\) \(=\lambda _{\delta }\)  (màu tím )

+ Còn ứng với những mức năng lương cao hơn thế nữa, ví dụ từ n \ ( \ geq \ ) 7 \ ( \ rightarrow \ ) m = 2 thì bước sóng nằm trong vùng tử ngoại. Và bước sóng ngắn nhất của dãy ứng với ngưyên tử di dời từ vô cùng ( n = \ ( \ infty \ ) ) về mức 2 : \ ( \ frac { 1 } { \ lambda_ { \ infty 2 } } = R_ { H } \ left ( \ frac { 1 } { 2 ^ { 2 } } – \ frac { 1 } { \ infty ^ { 2 } } \ right ) \ Rightarrow \ lambda_ { \ infty 2 } = \ frac { 1 } { R_ { H } \ left ( \ frac { 1 } { 2 ^ { 2 } } – \ frac { 1 } { \ infty ^ { 2 } } \ right ) } = 3,645068. 10 ^ { – 7 } m \ ) \ ( \ approx 0,365 \ mu m \ )Hay \ ( \ frac { hc } { \ lambda _ { \ infty } } = E_ { \ infty } – E_ { 2 } \ Rightarrow \ lambda _ { \ infty } = 0,365 \ mu m \ )Vậy, Các bức xạ trong dãy Balmer có một phần nằm trong vùng tử ngoại và một phần nằm trong vùng ánh sáng nhìn thấy. Phần nhìn thấy này có 4 vạch là : Đỏ : \ ( H_ { \ alpha } ( \ lambda _ { \ alpha } = 0,656 \ mu m ) \ ) ; lam : \ ( H_ { \ beta } ( \ lambda _ { \ beta } = 0,486 \ mu m ) \ ) ; chàm : \ ( H_ { \ gamma } ( \ lambda _ { \ gamma } = 0,434 \ mu m ) \ ) ; tím : \ ( H_ { \ delta } ( \ lambda _ { \ delta } = 0,410 \ mu m ) \ )

Ví dụ 3  về các bước sóng dãy Paschen ( Hồng ngoại)

Các bức xạ trong dãy Paschen thuộc vùng hồng ngoại trong thang sóng điện từTa đã biết : trong mẫu nguyên tử Bor thì : \ ( E_ { n } = \ frac { E_ { 0 } } { n ^ { 2 } } = – \ frac { 13,6 } { n ^ { 2 } } ( eV ) \ ) với n = 1, 2, 3, 4 …những bức xạ thuộc dãy Paschen ứng với trường hợp nguyên tử từ mức cao hơn trở về mức 3+ Vạch tiên phong có bước sóng lớn nhất ứng với mức năng lương n = 4 \ ( \ rightarrow \ ) m = 3theo Anh xtanh : \ ( \ frac { hc } { \ lambda _ { 43 } } = E_ { 4 } – E_ { 3 } \ Rightarrow \ lambda _ { 43 } = 0,83 \ mu m \ )+ Vạch sau cuối có bước sóng ngắn nhất ứng với mức năng lương n = \ ( \ infty \ ) \ ( \ rightarrow \ ) m = 3theo Anh xtanh : \ ( \ frac { hc } { \ lambda _ { \ infty 3 } } = E_ { \ infty } – E_ { 3 } \ Rightarrow \ lambda _ { \ infty 3 } = 0,78 \ mu m \ )Vậy bước sóng thuộc dãy Paschen nằm trong khoảng chừng 0,78 \ ( \ mu m \ ) < l < 0,83 \ ( \ mu m \ ) nên nó thuộc vùng hồng ngoại .

3.Các dạng bài tập:  

DẠNG 1: Tìm năng lượng của một photon, tần số hay bước sóng:

Hướng dẫn: Áp dụng công thức \(e=hf=\frac{hc}{l}\)  hay \(E_{cao}-E_{thấp}=hf\) để suy ra các đại lượng chưa biết.

Ví dụ 1: Chiếu một chùm sáng đơn sắc có bước sóng bằng 0,72\(\mu m\). Tìm tần số và năng lượng photon?

HD Giải :  Áp dụng công thức \(f=\frac{c}{\lambda }\)  và \(e=hf=\frac{hc}{l}\)

Ví dụ 2:   Êlectron trong nguyên tử hiđrô chuyển từ mức năng lượng thứ 3 về mức năng lượng thứ nhất. Tính năng lượng phôtôn phát ra và tần số của phôtôn đó. Cho biết năng lượng của nguyên tử hiđro ở mức năng lượng thứ n là               En = – \(\frac{13,6}{n^{2}}(eV)\) Hằng số Plăng h = 6,625.10-34 (J.s)

HD Giải : Tính \(\Delta E\) và f của phôtôn.

Năng lượng của phôtôn phát ra : \ ( \ Delta E = E_ { 3 } – E_ { 1 } = – 13,6 \ left ( \ frac { 1 } { 3 ^ { 2 } } – \ frac { 1 } { 1 ^ { 2 } } \ right ) = 12,088 ( eV ) \ ) Tần số xê dịch của phôtôn : \ ( f = \ frac { \ Delta E } { h } \ approx 2,92. 10 ^ { 15 } ( Hz ) \ )

DẠNG 2:  Tìm động năng cực đại của electron khi xảy ra hiên tượng quang điện:

Hướng dẫn: Công thức: \(e=hf=\frac{hc}{\lambda }=A+\frac{mv_{0Max}^{2}}{2}\) với Eđ \(=\frac{mv_{Max}^{2}}{2}\) từ đó suy ra Eđ.                          Lưu ý: 1eV=1,6.10-19J

Ví dụ 1:  Catốt của tế bào quang điện làm bằng vônfram, biết công thoát của electron với vônfram là 7,2.10-19J. Chiếu vào catốt ánh sáng có bước sóng \(\lambda =0,18\mu m\). Động năng cực đại của êlectrôn khi bức ra khỏi catôt là bao nhiêu?

HD Giải:  Công thức \(e=hf=\frac{hc}{\lambda }=A+\frac{mv_{0Max}^{2}}{2}\) với Eđ \(=\frac{mv_{Max}^{2}}{2}\) Từ đó ta suy ra Eđmax

Mở rộng : bài toán tương tự như tìm Vmax ta cũng tìm Eđmax …

DẠNG 3: Tìm vận tốc cực đại của electron khi đập vào catot.

Hướng dẫn: Vận dụng công thức: Eđ = A = |e|UAK là năng lượng do điện trường cung cấp: |e|UAK = Ed = \(\frac{mv^{2}}{2}\)         Từ đó suy ra được v

Ví dụ 1:  Hiệu điện thế giữa Anot và catot của ống Culitzơ là 20kV. Cho e = 1,6.10-19C, h=6,625.10-34Js, c=3.108m/s. Bỏ qua động năng ban đầu của electron. Tính vận tốc của electron khi đập vào catot?

HD Giải:  Vận dụng công thức  Eđ = A = |e| UAK và |e|UAK = Eđ = mv2/2. Ta có v=8,4.107m/s.

DẠNG 4: Tìm số electron bay ra khỏi anot, số photon đập vào anot trong một thời gian t bất kỳ. Tìm hiệu suất quang điện.

Hướng dẫn:

– Tìm số electron bay ra khỏi catot là số electron tạo ra dòng quang điện do vậy ta vận dụng công thức : \ ( I = \ frac { q } { t } = \ frac { n_ { e } \ begin { vmatrix } e \ end { vmatrix } } { t } \ ) từ đó suy ra ne

– Tìm số photon đập vào anot : Ta tìm nguồn năng lượng của chùm photon và lấy nguồn năng lượng của chùm photon chia cho nguồn năng lượng của một photon thì ta có số photon cần tìm. Với bài toán này đề thường cho hiệu suất bức xạ P. nên ta có : \ ( n_ { p } = \ frac { A_ { p } } { \ varepsilon } = P. \ frac { t } { hf } \ )- Muốn tìm hiện suất quang điện ta dùng công thức : \ ( H = \ frac { n_ { e } } { n_ { p } } \ )

Ví dụ 1: : Chiếu một chùm bức xạ vào tế bào quang điện có catot làm bằng Na thì cường độ dòng quang điện bão hòa là 3. Số electron bị bứt ra ra khỏi catot trong hai phút là bao nhiêu?

HD Giải: Áp dụng công thức \(I=\frac{q}{t}=\frac{n_{e}\begin{vmatrix} e \end{vmatrix}}{t}\)  ta suy ra được \(n_{e}=I.\frac{t}{\begin{vmatrix} e \end{vmatrix}}\). Lưu ý đổi đơn vị của I ra ampe       

Ví dụ 2:  Chiếu vào catốt một ánh sáng có bước sóng 0,546μm, thì dòng quang điện bảo hoà có giá trị là 2mA. Công suất bức xạ là 1,515W. Hiệu suất lượng tử là bao nhiêu ?.

HD Giải :  Áp dụng công thức : \(I=\frac{q}{t}=\frac{n_{e}\begin{vmatrix} e \end{vmatrix}}{t}\)  ta tìm được ne; công thức \(n_{p}=\frac{A_{p}}{\varepsilon }=P.\frac{t}{hf}\) ta tìm được np và công thức \(H=\frac{n_{e}}{n_{p}}\)  để tìm H. Lưu ý: H tính ra %

DẠNG 5: Tìm hiệu điện thế hãm để không một electron bay về anot (hay dòng quang điện triệt tiêu)

Hướng dẫn: – Hiện tượng các electron không về được anot do điện trường sinh công cản cản trở chúng.

– Muốn vậy thì : Công cản điện trường có giá trị bé nhất bằng động năng bắt đầu cực lớn của những electron quang điện. Ta có : \ ( \ begin { vmatrix } eU_ { h } \ end { vmatrix } = \ frac { mv_ { 0M ax } ^ { 2 } } { 2 } \ Rightarrow U_ { h } = \ frac { mv_ { 0M ax } ^ { 2 } } { 2 \ begin { vmatrix } e \ end { vmatrix } } \ )- Lưu ý : Khi chọn hiệu quả thì Uh < 0. Trong bài toán trắc nghiệm nếu không có giá trị âm thì chọn giá trị độ lớn .

Ví dụ 1:  Chiếu một ánh sáng có bước sóng 0,45μm vào catot của một tế bào quang điện. Công thoát kim loại làm catot là 2eV. Tìm hiệu điện thế giữa anot và catot để dòng quang điện triệt tiêu?

HD Giải:  Vận dụng \(U_{h}=\frac{mv_{0Max}^{2}}{2\begin{vmatrix} e \end{vmatrix}}\)  nhưng ta phải tìm Eđ = \(\varepsilon\) – A. Với Eđ = \(\frac{1}{2}mv_{0}^{2}\) Từ đó ta tìm được Uh = -0,76V

DẠNG 6: Xác định bước sóng ánh sáng (hay tần số) mà photon phát ra trong quá trình nguyên tử chuyển từ quỹ đạo có năng lượng cao về quỹ đạo có mức năng lượng thấp hơn.

Hướng dẫn:

– Khi chuyển từ mức nguồn năng lượng cao về mức thấp thì nguyên tử phát ra photon có nguồn năng lượng : \ ( e = hf_ { nm } = \ frac { hc } { l_ { nm } } = E_ { n } – E_ { n } ( E_ { n } > E_ { m } ) \ ) ( 10 ) từ đó suy ra được bước sóng hay tần số .- Lưu ý : thường ta lên vẽ biểu đồ mức lượng để giải .

Ví dụ 1:  Nguyên tử Hydro bị kích thích chuyển lên quỹ đạo có năng lượng cao. Sau đó chuyển từ quỹ đạo có lượng E3 về E1 thì phát ra ánh sáng đơn sắc có tần số f31 = 4200Hz. Khi chuyển từ E3 về E2 thì phát ra ánh sáng đơn sắc có tần số f32 = 3200Hz. Tìm tần số ánh sáng khi nó chuyển từ mức năng lượng E2 về E1?                          HD Giải :  Vận dụng công thức \(e=hf_{nm}=\frac{hc}{l_{nm}}=E_{n}-E_{n}(E_{n}>E_{m} )\) (10) 

ta có : E3 – E1 = ( E3 – E2 ) + ( E2 – E1 ) \ ( \ Leftrightarrow \ ) hf31 = hf32 + hf21 \ ( \ Leftrightarrow \ ) f31 = f32 + f21 Suy ra : f21 = f31 – f32Mở rộng : Nếu tìm bước sóng ta cũng có : \ ( \ frac { 1 } { \ lambda _ { 31 } } = \ frac { 1 } { \ lambda _ { 32 } } + \ frac { 1 } { \ lambda _ { 21 } } \ ) từ đây suy ra những bước sóng cần tìm .

Ví dụ 2:  Trong quang phổ hiđrô, bước sóng λ (μm) của các vạch quang phổ như sau: Vạch thứ nhất của dãy Lai-man λ21 =0,1216 μm; Vạch Hα của dãy Ban-me λ­Hα = 0,6563μm.Vạch đầu của dãy Pa-sen λ43 =1,8751μm

Tính bước sóng của hai vạch quang phổ thứ hai, thứ ba của dãy Lai-man và của vạch Hβ .

HD Giải: Áp dụng công thức \(\frac{1}{\lambda _{mn}}=\frac{E_{m}-E_{N}}{hc}\) với m > n .

Dãy Lai-man : \ ( \ frac { 1 } { \ lambda _ { 31 } } = \ frac { E_ { 3 } – E_ { 1 } } { hc } = \ frac { E_ { 3 } – E_ { 2 } } { hc } + \ frac { E_ { 2 } – E_ { 1 } } { hc } = \ frac { 1 } { \ lambda _ { 32 } } + \ frac { 1 } { \ lambda _ { 21 } } \ Rightarrow \ lambda _ { 31 } = 0,1026 ( \ mu m ) \ )\ ( \ frac { 1 } { \ lambda _ { 42 } } = \ frac { 1 } { \ lambda _ { 43 } } + \ frac { 1 } { \ lambda _ { 32 } } \ Rightarrow \ lambda _ { 42 } = 0,4861 ( \ mu m ) \ )

4.Bài tập có lời giải hoặc hướng dẫn:

Bài 1. Bước sóng của vạch quang phổ đầu tiên trong dãy Laiman là λ0 = 122 nm, của hai vạch Ha và Hb trong dãy Banme lần lượt là λ1 = 656nm và λ2 = 486 nm. Hãy tính bước sóng của vạch quang phổ thứ hai trong dãy Laiman và vạch đầu tiên trong dãy Pasen.

HD Giải: \(\frac{hc}{\lambda _{31}}=E_{3}-E_{1}=E_{3}-E_{2}+E_{2}-E_{1}=\frac{hc}{\lambda _{1}}+\frac{hc}{\lambda _{0}}\Rightarrow\lambda _{31}=\frac{\lambda _{0}\lambda _{1}}{\lambda _{0}+\lambda _{1}} =103nm\) 

\ ( \ frac { hc } { \ lambda _ { 43 } } = E_ { 4 } – E_ { 3 } = E_ { 4 } – E_ { 2 } + E_ { 2 } – E_ { 3 } = \ frac { hc } { \ lambda _ { 2 } } + \ frac { hc } { \ lambda _ { 1 } } \ Rightarrow \ lambda _ { 43 } = \ frac { \ lambda _ { 1 } \ lambda _ { 2 } } { \ lambda _ { 1 } + \ lambda _ { 2 } } = 1875 nm \ )

Bài 2. Trong quang phổ vạch của nguyên tử hiđrô, vạch ứng với bước sóng dài nhất trong dãy Laiman là <

Tất cả nội dung bài viết. Các em hãy xem thêm và tải file chi tiết dưới đây:

Xem thêm: Phần mềm hóa đơn điện tử, hóa đơn điện tử xác thực – Nhân Hòa

2k6 tham gia ngay Group Zalo chia sẻ tài liệu ôn thi và hỗ trợ học tập

Luyện Bài tập trắc nghiệm môn Vật lý lớp 12 – Xem ngay

Source: https://vh2.com.vn
Category : Điện Tử