Phương pháp giải một số dạng bài tập Đại cương về dòng điện xoay chiều | SGK Vật lí lớp 12

Dạng 1: Xác định từ thông qua khung dây và suất điện động xoay chiều

Sử dụng những công thức :

– Từ thông:

Bạn đang đọc: Phương pháp giải một số dạng bài tập Đại cương về dòng điện xoay chiều | SGK Vật lí lớp 12

\ ( \ Phi = NB { \ rm { S } } \ cos \ left ( { \ omega t + \ varphi } \ right ) = { \ Phi _0 } \ cos \ left ( { \ omega t + \ varphi } \ right ) \ ) ( Wb )Trong đó :+ N : số vòng dây+ S : tiết diện vòng dây ( mét vuông )+ B : cảm ứng từ ( T )+ \ ( { \ Phi _0 } = NB { \ rm { S } } \ ) : từ thông cực đại qua khung dây ( Wb )+ \ ( \ omega \ ) : vận tốc quay của khung dây ( rad / s )- Suất điện động xoay chiều :\ ( e = – \ Phi ‘ = { E_0 } \ cos \ left ( { \ omega t + \ varphi } \ right ) \ ) ( V )Trong đó : \ ( { E_0 } = NB { \ rm { S } } \ omega = \ omega { \ Phi _0 } \ ) : suất điện động xoay chiều cực lớn ( V )

*Chú ý: Khi trong khung dây có suất điện động thì hai đầu khung dây có điện áp (hiệu điện thế). Nếu khung dây chưa nối với tải thì E = U.

Bài tập ví dụ: Từ thông qua một vòng dây dẫn là \(\Phi  = \frac{{{{2.10}^{ – 2}}}}{\pi }\cos \left( {100\pi t + \frac{\pi }{4}} \right)\left( {{\rm{W}}b} \right)\). Biểu thức của suất điện động cảm ứng xuất hiện trong vòng dây này là?

Hướng dẫn giải

Ta có :\ ( e = – \ Phi ‘ = \ omega { \ Phi _0 } \ sin \ left ( { \ omega t + \ varphi } \ right ) \ \ = \ omega { \ Phi _0 } \ cos \ left ( { \ omega t + \ varphi – \ frac { \ pi } { 2 } } \ right ) \ )\ ( \ Rightarrow e = \ frac { { { { 2.10 } ^ { – 2 } } } } { \ pi }. 100 \ pi \ cos \ left ( { 100 \ pi t + \ frac { \ pi } { 4 } – \ frac { \ pi } { 2 } } \ right ) \ \ = 2 \ cos \ left ( { 100 \ pi t – \ frac { \ pi } { 4 } } \ right ) \ left ( V \ right ) \ )

Dạng 2: Xác định các đại lượng đặc trưng của dòng điện xoay chiều

– Phương trình tổng quát của dòng điện xoay chiều :\ ( i = { I_0 } \ cos \ left ( { \ omega t + \ varphi } \ right ) \ ), với I0 là cường độ dòng điện cực lớn .- Các giá trị hiệu dụng :+ Cường độ dòng điện hiệu dụng : \ ( I = \ frac { { { I_0 } } } { { \ sqrt 2 } } \ )

+ Suất điện động hiệu dụng : \ ( E = \ frac { { { E_0 } } } { { \ sqrt 2 } } \ )+ Điện áp hiệu dụng : \ ( U = \ frac { { { U_0 } } } { { \ sqrt 2 } } \ )- Nhiệt lượng tỏa ra trên điện trở R : \ ( Q = { I ^ 2 } Rt \ )Trong đó :Q. : nhiệt lượng ( J )

R: điện trở mạch ngoài

Xem thêm: Bài giảng điện tử là gì? Phân biệt bài giảng điện tử và giáo án điện tử

t : thời giam dòng điện chạy qua R ( s )- Công suất tỏa nhiệt : \ ( P = \ frac { Q } { t } = { I ^ 2 } R \ ) ( W )

Bài tập ví dụ:

Cường độ dòng điện \ ( i = 2 \ sqrt 2 \ cos \ left ( { 100 \ pi t } \ right ) \ left ( A \ right ) \ ) có giá trị hiệu dụng là bao nhiêu ?

Hướng dẫn giải

Từ phương trình ta có cường độ dòng điện cực đại \ ( { I_0 } = 2 \ sqrt 2 A \ )Cường độ dòng điện hiệu dụng :\ ( I = \ frac { { { I_0 } } } { { \ sqrt 2 } } = \ frac { { 2 \ sqrt 2 } } { { \ sqrt 2 } } = 2A \ )

Dạng 3: Tìm điện lượng chuyển qua tiết diện dây dẫn

Điện lượng qua tiết diện S trong thời hạn t là q : \ ( q = i. t \ )Điện lượng qua tiết diện S trong thời hạn từ t1 đến t2 là \ ( \ Delta q \ ) : \ ( \ Delta q = i. \ Delta t \ )

\ ( \ Rightarrow i = \ dfrac { { dq } } { { dt } } \ Rightarrow q = \ int \ limits_ { { t_1 } } ^ { { t_2 } } { i { \ rm { d } } t } \ )

Bài tập ví dụ:

Dòng điện xoay chiều có biểu thức : \ ( i = 2 \ sin 100 \ pi t \ left ( A \ right ) \ ) chạy qua dây dẫn. Điện lượng chạy qua tiết diện dây trong khoảng chừng thời hạn từ 0 đến 0,15 s là :

Hướng dẫn giải

Ta có :\ ( \ Rightarrow i = \ dfrac { { dq } } { { dt } } \ Rightarrow q = \ int \ limits_ { { t_1 } } ^ { { t_2 } } { i { \ rm { d } } t } = \ int \ limits_0 ^ { 0,15 } { 2 \ sin 100 \ pi tdt } \ )\ ( \ Rightarrow q = – \ dfrac { { 2 \ cos 100 \ pi t } } { { 100 \ pi } } \ left | { _0 ^ { 0,15 } } \ right. = \ dfrac { 4 } { { 100 \ pi } } \ left ( C \ right ) \ )

Dạng 4: Tính số lần dòng điện đổi chiều sau một khoảng thời gian t

Trong mỗi giây: Dòng điện đổi chiều 2f lần

=> Trong thời gian t giây: Dòng điện đổi chiều t.2f  lần

Đặc biệt: Nếu pha ban đầu \({\varphi _i} = \frac{\pi }{2}\) hoặc \({\varphi _i} =  – \frac{\pi }{2}\)thì chỉ giây đầu tiên đổi chiều 2f-1 lần

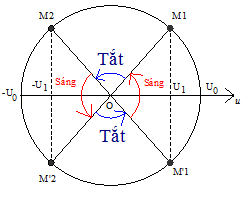
 Dạng 5: Xác định thời gian đèn sáng – tắt.

– Dùng mối liên hệ giữa xê dịch điều hòa và hoạt động tròn đều để tính .- Dòng điện xoay chiều :

• Mỗi giây dòng điện đôi chiều 2f lần.
• Nếu cho dòng điện qua bộ phận làm rung dây trong hiện tượng sóng dừng thì dây rung với tần số 2f.

– Công thức tính thời hạn đèn huỳnh quang sáng trong 1 chu kì .

Khi đặt điện áp u = U0cos(wt + ju) vào hai đầu bóng đèn, biết đèn chỉ sáng lên khi u ≥ U1.

Xem thêm: Hướng dẫn kê khai thuế điện tử – Đại lý Thuế Việt An

\ ( \ Delta t = \ frac { { 4 \ Delta \ varphi } } { \ omega } \ ) Với \ ( c { \ rm { os } } \ Delta \ varphi = \ frac { { { U_1 } } } { { { U_0 } } } \ ), \ ( ( 0 { \ rm { } } < \ Delta \ varphi < \ frac { \ pi } { 2 } ) \ )

Source: https://vh2.com.vn
Category : Điện Tử