Giải Cùng em học Toán lớp 5 tập 2 tuần 19 câu 1, 2, 3, 4 trang 5, 6

Lựa chọn câu để xem giải thuật nhanh hơn

Bài 1

Bạn đang đọc: Giải Cùng em học Toán lớp 5 tập 2 tuần 19 câu 1, 2, 3, 4 trang 5, 6

Tính diện tích quy hoạnh hình thang :
a ) Có độ dài hai đáy lần lượt là 21 cm ; 14 m ; chiều cao 10 cm .
b ) Có độ dài hai đáy lần lượt là 7,2 m ; 4,8 m ; chiều cao 5 m .

Phương pháp giải:

Để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho \(2\) (cùng một đơn vị đo).

Lời giải chi tiết:

a ) Đổi : \ ( 14 m = 1400 cm \ ) .
Diện tích hình thang đó là :
\ ( ( 21 + 1400 ) \ times 10 : 2 = 7105 \, \, ( c { m ^ 2 } ) \ )
b ) Diện tích hình thang đó là :
\ ( ( 7,2 + 4,8 ) \ times 5 : 2 = 30 \, \, ( { m ^ 2 } ) \ )
Đáp số : a ) \ ( 7105 c { m ^ 2 } \ ) ;
b ) \ ( 30 { m ^ 2 } \ ).

Bài 2

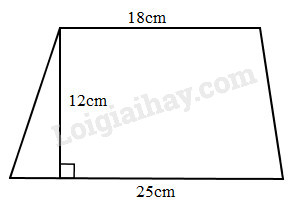
Tính diện tích quy hoạnh mảnh bìa hình thang có size như hình vẽ :

Phương pháp giải:

Hình thang đã cho là hình thang có chiều cao là \(12cm\),  độ dài hai đáy là \(18cm\) và \(25cm\). Để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho \(2\).

Lời giải chi tiết:

Diện tích hình thang đó là :
\ ( ( 18 + 25 ) \ times 12 : 2 = 258 \, \, ( c { m ^ 2 } ) \ )
Đáp số : \ ( 258 c { m ^ 2 }. \ )

Bài 3

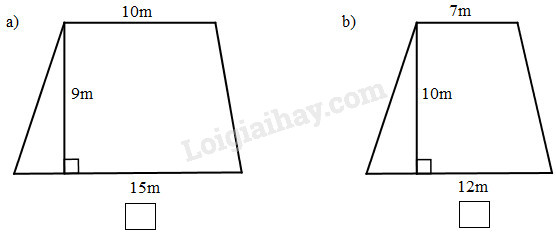
Đánh dấu ( × ) vào ô trống dưới hình thang có diện tích quy hoạnh nhỏ hơn 100 mét vuông .

Phương pháp giải:

– Xác định độ dài hai đáy và chiều cao của hình thang rồi tính diện tích quy hoạnh hai hình thang .

– Để tính diện tích ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho \(2\).

Lời giải chi tiết:

Hình thang a có chiều cao là \ ( 9 m \ ), độ dài hai đáy là \ ( 10 m \ ) và \ ( 15 m \ ) .
Hình thang b có chiều cao là \ ( 10 m \ ), độ dài hai đáy là \ ( 7 m \ ) và \ ( 12 m \ ) .
Diện tích hình thang a là :
\ ( ( 10 + 15 ) \ times 9 : 2 = \, \, 112,5 \, \, ( { m ^ 2 } ) \ )
Diện tích hình thang b là :
\ ( ( 7 + 12 ) \ times 10 : 2 = 95 \, \, ( { m ^ 2 } ) \ )
Ta có : \ ( 112,5 c { m ^ 2 } > 100 c { m ^ 2 } \ ) ; \ ( 95 c { m ^ 2 } < 100 c { m ^ 2 } \ ) . Vậy hình thang b có diện tích quy hoạnh nhỏ hơn \ ( 100 c { m ^ 2 } \ ).

Bài 4

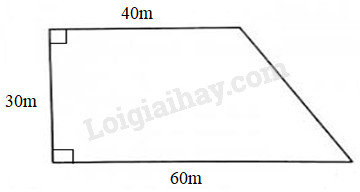
Trên một thửa ruộng hình thang với những kích cỡ được miêu tả như hình vẽ dưới đây, người ta trồng rau cải bắp hết \ ( 30 \ % \ ) diện tích quy hoạnh. Tính số ki-lô-gam cải bắp thu hoạch được, biết mỗi mét vuông thu hoạch được \ ( 10 kg \ ) bắp cải .

Phương pháp giải:

– Quan sát hình vẽ để tìm chiều dài, chiều rộng và chiều cao của thửa ruộng hình thang .

– Tính diện tích thửa ruộng ta lấy tổng độ dài hai đáy nhân với chiều cao rồi chia cho \(2\).

– Tính diện tích quy hoạnh trồng bắp cải ta lấy diện tích quy hoạnh thửa ruộng chia cho \ ( 100 \ ) rồi nhân với \ ( 30 \ ) .
– Tính số ki-lô-gam rau thu được ta lấy số ki-lô-gam rau thu được ở 1 mét vuông nhân với diện tích quy hoạnh trồng bắp cải .

Lời giải chi tiết:

Diện tích của thửa ruộng đó là :
\ ( ( 40 + 60 ) \ times 30 : 2 = 1500 \ ) \ ( ( m ^ 2 ) \ )
Diện tích trồng rau bắp cải là :
\ ( 1500 : 100 \ times 30 = 450 \ ; ( m ^ 2 ) \ )
Số ki-lô-gam cải bắp thu hoạch được là :
\ ( 10 \ times 450 = 4500 \ ; ( kg ) \ )
Đáp số : \ ( 4500 kg \ ) .

Loigiaihay.com

Bài 5

Viết tiếp vào chỗ chấm cho thích hợp .

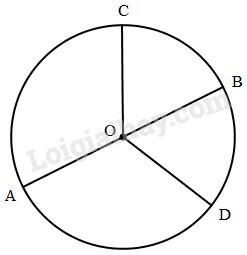
a ) Tâm của đường tròn là : … …
b ) Các nửa đường kính của hình tròn trụ là : … …

c) Đường kính của hình tròn là: …….

Xem thêm: 221+ Tranh doanh nhân tạo động lực làm việc hiệu quả

d ) Nếu OA = 3 cm thì OB = … ; OC = … ; OD = … ; AB = …

Phương pháp giải:

Quan sát hình vẽ để tìm tâm, nửa đường kính, đường kính của hình tròn trụ đã cho .

Lời giải chi tiết:

a ) Tâm của đường tròn là \ ( O \ ) .
b ) Các nửa đường kính của hình tròn trụ là \ ( OA, \, \, OB, \, \, OC, \, \, OD \ ) .
c ) Đường kính của đường tròn là \ ( AB \ ) .
d ) Nếu \ ( OA = 3 cm \ ) thì \ ( OB = 3 cm ; \ ) \ ( OC = 3 cm ; \ ) \ ( OD = 3 cm ; \ ) \ ( AB = 6 cm \ ).

Bài 6

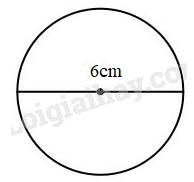
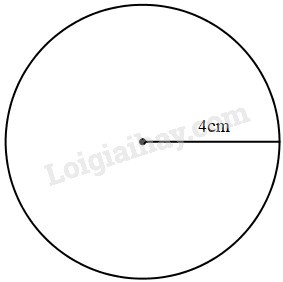
Vẽ hình tròn trụ :
a ) Đường kính 6 cm ;
b ) Bán kính 4 cm .

Phương pháp giải:

Câu a : Tính nửa đường kính : 6 : 2 = 3 cm .
+ ) Cách vẽ
– Chấm một điểm, ví dụ điển hình O ( hoặc I ), làm tâm .
– Mở compa sao cho mũi kim cách đầu chì một khoảng chừng 3 cm ( hoặc 4 cm ) .
– Đặt mũi kim vào điểm O, áp đầu chì sát vào mặt giấy quay đúng một vòng. Ta được hình tròn trụ tâm O ( hoặc I ) có nửa đường kính 3 cm ( hoặc 4 cm ) .

Lời giải chi tiết:

a ) Bán kính hình tròn trụ là : 6 : 2 = 3 ( cm )

b ) Bán kính 4 cm .

Bài 7

Tính chu vi hình tròn trụ :
a ) Có đường kính 8 cm ;
b ) Có nửa đường kính 5 m .

Phương pháp giải:

Dựa vào quy tắc tính chu vi hình tròn trụ :
– Muốn tính chu vi hình tròn trụ ta lấy đường kính nhân với số \ ( 3,14 \ ) .
– Muốn tính chu vi hình tròn trụ ta lấy \ ( 2 \ ) lần nửa đường kính nhân với số \ ( 3,14 \ ) .

Lời giải chi tiết:

a ) Chu vi hình tròn trụ có đường kính 8 cm là :
\ ( 8 \ times 3,14 = 25,12 \, \, ( cm ) \ )
b ) Chu vi hình tròn trụ có nửa đường kính 5 m là :
\ ( 5 \ times 2 \ times 3,14 = 31,4 \, \, ( m ) \ )
Đáp số : a ) \ ( 25,12 cm \ ) ;
b ) \ ( 31,4 m \ ).

Bài 8

Một mặt bàn hình tròn trụ có đường kính là 13,5 dm. Tính chu vi mặt bàn đó .

Phương pháp giải:

Muốn tính chu vi mặt bàn hình tròn trụ ta lấy đường kính nhân với số \ ( 3,14 \ ) .

Lời giải chi tiết:

Chu vi mặt bàn đó là :
\ ( 13,5 \ times 3,14 = 42,39 \, \, ( dm ) \ )
Đáp số : \ ( 42,39 \, dm \ ).

Vui học

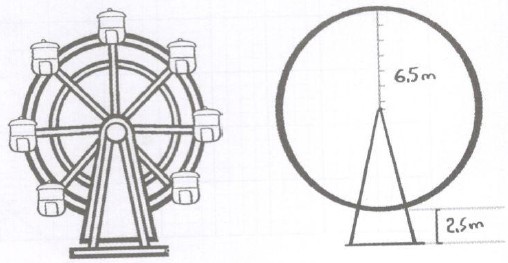
Vòng quay ở một khu vui chơi giải trí công viên có kích cỡ được mô phỏng như hình vẽ bên. Nếu bạn Hùng đang ở vị trí cao nhất của vòng xoay thì bạn Hùng cách mặt đất bao nhiêu mét ? Vì sao ?

Phương pháp giải:

Khoảng cách của Hùng khi ở vị trí cao nhất của vòng xoay so với mặt đất bằng tổng của đường kính vòng xoay và \ ( 2,5 m \ ) .

Lời giải chi tiết:

Quan sát hình vẽ ta thấy vòng xoay có nửa đường kính là \ ( 6,5 m \ ) .
Đường kính của vòng xoay đó là :
\ ( 6,5 \ times 2 = 13 \, \, ( m ) \ )
Nếu bạn Hùng ở vị trí cao nhất của vòng xoay thì bạn Hùng cách mặt đất số mét là :
\ ( 13 + 2,5 = 15,5 \, \, ( m ) \ )

                             Đáp số : \(15,5m\).

Xem thêm: LỄ KỶ NIỆM 15 NĂM NGÀY DOANH NHÂN VIỆT NAM 2019

 Loigiaihay.com

Source: https://vh2.com.vn
Category : Doanh Nhân